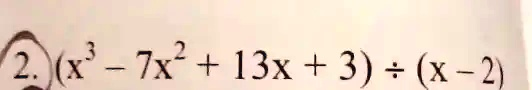
The Correct Answer and Explanation is:
The expression to simplify is:
(x3−7×2+13x+3)÷(x−2)(x^3 – 7x^2 + 13x + 3) \div (x – 2)
Correct Answer:
The result of the division is:
(x3−7×2+13x+3)÷(x−2)=x2−5x+3+9x−2(x^3 – 7x^2 + 13x + 3) ÷ (x – 2) = x^2 – 5x + 3 + \frac{9}{x – 2}
Explanation:
To divide a polynomial by a binomial, we can use polynomial long division.
First, divide the leading term x3x^3 by the leading term of the divisor xx, which gives x2x^2. Multiply x2x^2 by the divisor x−2x – 2, resulting in x3−2x2x^3 – 2x^2. Subtracting this from the original expression, we get a new polynomial:
(x3−7×2+13x+3)−(x3−2×2)=−5×2+13x+3(x^3 – 7x^2 + 13x + 3) – (x^3 – 2x^2) = -5x^2 + 13x + 3
Next, divide −5×2-5x^2 by xx, giving −5x-5x. Multiply −5x-5x by x−2x – 2, yielding −5×2+10x-5x^2 + 10x. Subtracting again:
(−5×2+13x+3)−(−5×2+10x)=3x+3(-5x^2 + 13x + 3) – (-5x^2 + 10x) = 3x + 3
Then divide 3x3x by xx, which gives 33. Multiply 33 by x−2x – 2 to get 3x−63x – 6. Subtract:
(3x+3)−(3x−6)=9(3x + 3) – (3x – 6) = 9
The remainder is 9. Since this cannot be divided further by x−2x – 2, it becomes the fractional term of the final answer.
Thus, the quotient is x2−5x+3x^2 – 5x + 3 with a remainder of 9, making the complete answer:
x2−5x+3+9x−2x^2 – 5x + 3 + \frac{9}{x – 2}
This technique is crucial for simplifying rational expressions and understanding the behavior of polynomial functions when divided.
