Which shape has both acute angles and obtuse angles?
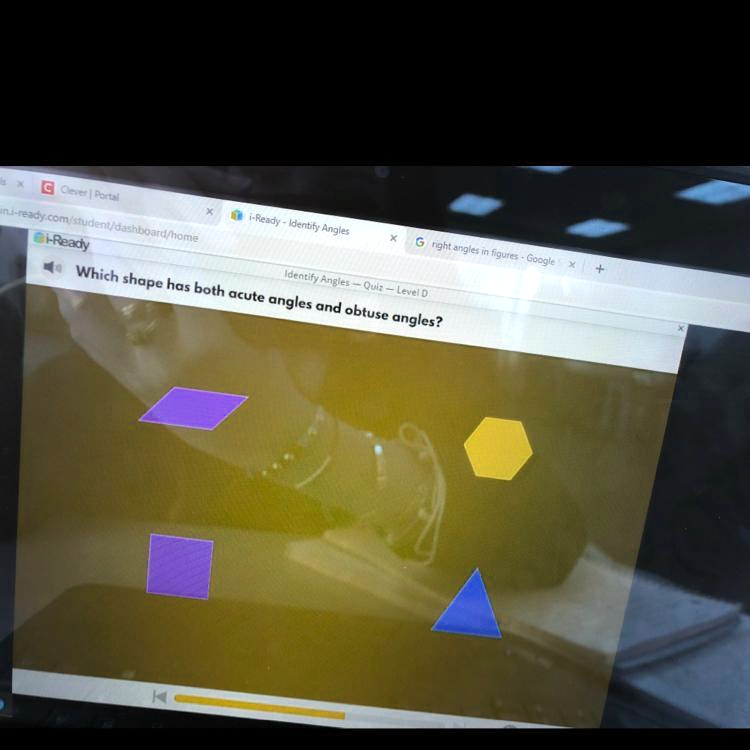
The shape that has both acute angles and obtuse angles is the purple parallelogram.
A parallelogram is a four-sided shape with opposite sides that are equal in length and parallel. One of the defining characteristics of a general parallelogram (excluding special types like rectangles and rhombi) is the presence of two different types of angles. Specifically, it has two acute angles and two obtuse angles. An acute angle measures less than 90 degrees while an obtuse angle measures more than 90 degrees but less than 180 degrees.
In the case of the purple parallelogram, each acute angle is paired with an adjacent obtuse angle, forming supplementary angle pairs. This means each acute and obtuse angle pair adds up to 180 degrees. Since opposite angles in a parallelogram are equal, the acute angles are congruent to each other, as are the obtuse angles.
This blend of angle types distinguishes the parallelogram from other options in the image. For instance, the triangle contains two acute angles and a right angle but lacks any obtuse angles. The hexagon shown appears to be regular with all interior angles measuring 120 degrees, which are obtuse, and thus it does not include any acute angles. The trapezoid might also have both acute and obtuse angles depending on the specific type, but based on the image, the parallelogram fits the requirement most clearly.
Understanding this kind of problem helps reinforce key concepts in geometry such as angle types, classifications of quadrilaterals, and properties of polygons. It also strengthens spatial reasoning, as one must visualize how angles behave within different shapes. Recognizing combinations of angle types in a shape prepares learners for more advanced topics like proofs, transformations, and congruency in geometric figures.
