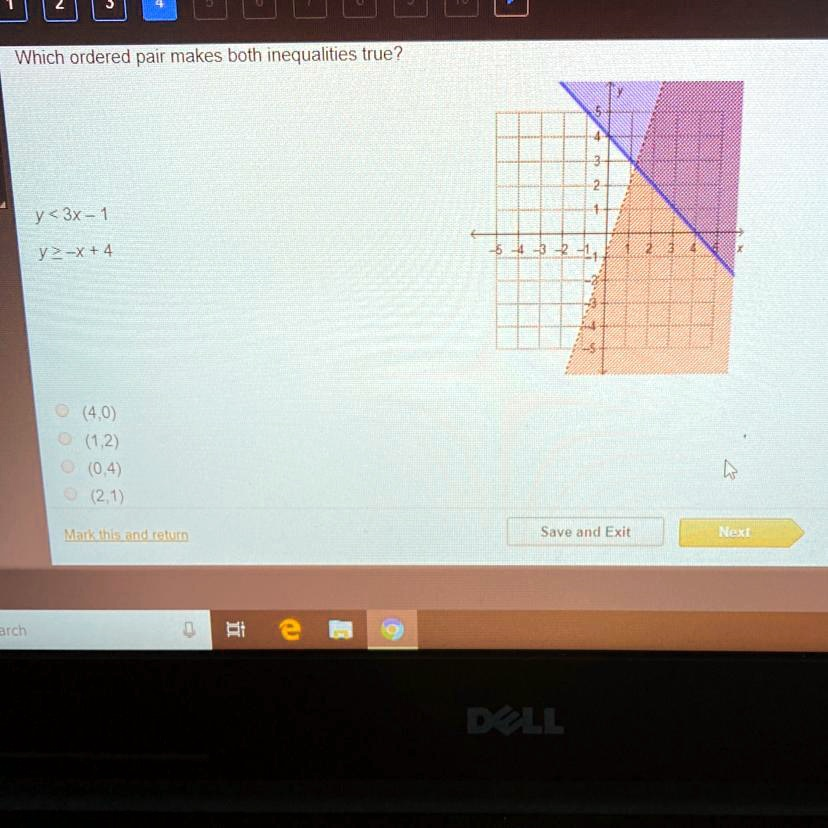
Which ordered pair makes both inequalities true? y < 3x – 1 y \geq -x + 4 (4,0) (1,2) (0,4) (2,1) Mark this and return
The Correct Answer and Explanation is:
To determine which ordered pair makes both inequalities true, we need to test each option by substituting its x and y values into both of the given inequalities. The two inequalities are:
- y < 3x – 1
- y ≥ -x + 4
A point is a solution to the system only if its coordinates satisfy both inequalities. Let’s check each ordered pair.
Option 1: (4, 0)
First, we substitute x = 4 and y = 0 into the first inequality:
0 < 3(4) – 1
0 < 12 – 1
0 < 11
This statement is true.
Next, we substitute x = 4 and y = 0 into the second inequality:
0 ≥ -(4) + 4
0 ≥ -4 + 4
0 ≥ 0
This statement is also true because the “or equal to” condition is met. Since (4, 0) satisfies both inequalities, it is a correct solution.
Option 2: (1, 2)
Substitute x = 1 and y = 2 into the first inequality:
2 < 3(1) – 1
2 < 3 – 1
2 < 2
This statement is false because 2 is not strictly less than 2. Therefore, (1, 2) is not a solution.
Option 3: (0, 4)
Substitute x = 0 and y = 4 into the first inequality:
4 < 3(0) – 1
4 < 0 – 1
4 < -1
This statement is false. Therefore, (0, 4) is not a solution.
Option 4: (2, 1)
Substitute x = 2 and y = 1 into the second inequality (we can start with either):
1 ≥ -(2) + 4
1 ≥ -2 + 4
1 ≥ 2
This statement is false. Therefore, (2, 1) is not a solution.
After testing all the options, the only ordered pair that makes both inequalities true is (4, 0). This point is located in the solution region of the graphed system.
The correct answer is (4, 0).
