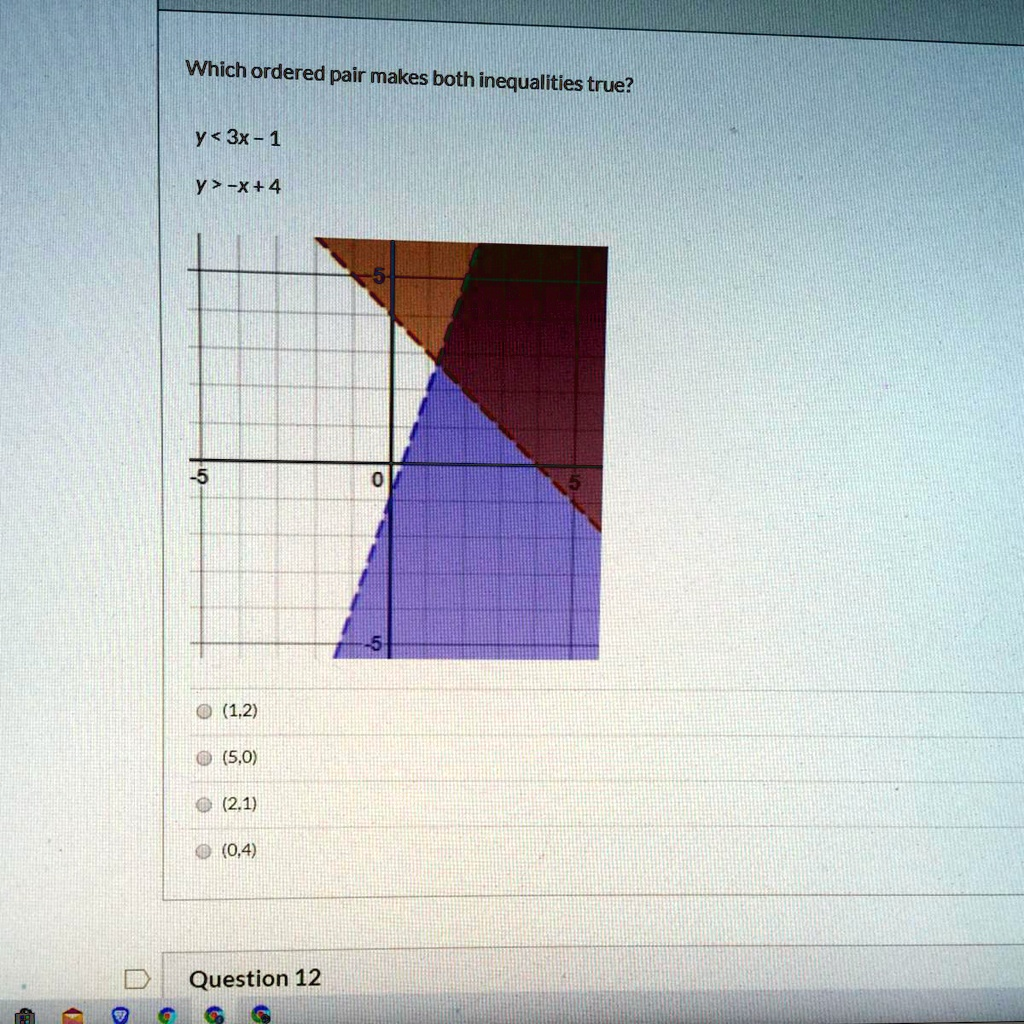
Which ordered pair makes both inequalities true? y < 3x – 1 y > -x + 4 (1,2) (5,0) (2,1) (0,4) Question 1
The Correct Answer and Explanation is:
To determine which ordered pair makes both inequalities true, we can test each point by substituting its x and y values into the two given inequalities: y < 3x – 1 and y > -x + 4. A point is a solution to the system only if it satisfies both conditions.
1. Testing the point (1, 2):
- For the first inequality, y < 3x – 1: Substitute x=1 and y=2.
2 < 3(1) – 1
2 < 3 – 1
2 < 2
This statement is false. Since the point (1, 2) does not satisfy the first inequality, it is not the correct answer.
2. Testing the point (5, 0):
- For the first inequality, y < 3x – 1: Substitute x=5 and y=0.
0 < 3(5) – 1
0 < 15 – 1
0 < 14
This statement is true. - Now, we check the second inequality, y > -x + 4:
0 > -(5) + 4
0 > -1
This statement is also true. - Because the point (5, 0) makes both inequalities true, it is a solution to the system.
3. Testing the point (2, 1):
- For the first inequality, y < 3x – 1: Substitute x=2 and y=1.
1 < 3(2) – 1
1 < 6 – 1
1 < 5
This statement is true. - Now, we check the second inequality, y > -x + 4:
1 > -(2) + 4
1 > 2
This statement is false. Therefore, (2, 1) is not the correct answer.
4. Testing the point (0, 4):
- For the second inequality, y > -x + 4: Substitute x=0 and y=4.
4 > -(0) + 4
4 > 4
This statement is false. A number cannot be strictly greater than itself. Thus, (0, 4) is not a solution.
The algebraic tests show that (5, 0) is the only ordered pair that satisfies both inequalities. The provided graph confirms this. The solution to a system of inequalities is the region where the shaded areas for each inequality overlap. In the graph, this is the dark maroon section. The point (5, 0) is the only option located within this overlapping solution area.
The correct ordered pair is (5, 0).
