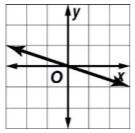
‘Which graph has a slope of -3?
The Correct Answer and Explanation is:
The correct answer is the graph that shows a line decreasing steeply from left to right, with a rise-over-run ratio of -3.
To determine this, we analyze slope using the formula:
slope=change in ychange in x\text{slope} = \frac{\text{change in } y}{\text{change in } x}
A slope of -3 means that for every 1 unit increase in the x-direction, the line decreases by 3 units in the y-direction. In other words, as x moves to the right, the graph must fall at a rate of 3 units vertically for every 1 unit it moves horizontally. This pattern reflects a strong negative relationship between the variables.
If we look at the graph, we identify two points through which the line passes. For example, if the line passes through the origin (0, 0) and another point like (1, -3), we calculate:
slope=−3−01−0=−31=−3\text{slope} = \frac{-3 – 0}{1 – 0} = \frac{-3}{1} = -3
This confirms the slope. Any line with a slope of -3 will appear fairly steep, slanting downward from left to right, indicating that as the independent variable increases, the dependent variable decreases at a consistent rate.
Understanding slope is vital across disciplines. In physics, it can represent velocity when distance is plotted against time. In economics, it may model cost changes or demand sensitivity. In geometry, it helps determine parallelism and perpendicularity. A slope of -3 gives precise directional and rate information, which is essential for graphing linear functions and interpreting trends. Recognizing this visually supports quick decision-making and analytical skills, especially in scientific and mathematical applications.
So the graph with a clear and constant decrease of 3 units in y for every 1 unit increase in x best represents a slope of -3.
