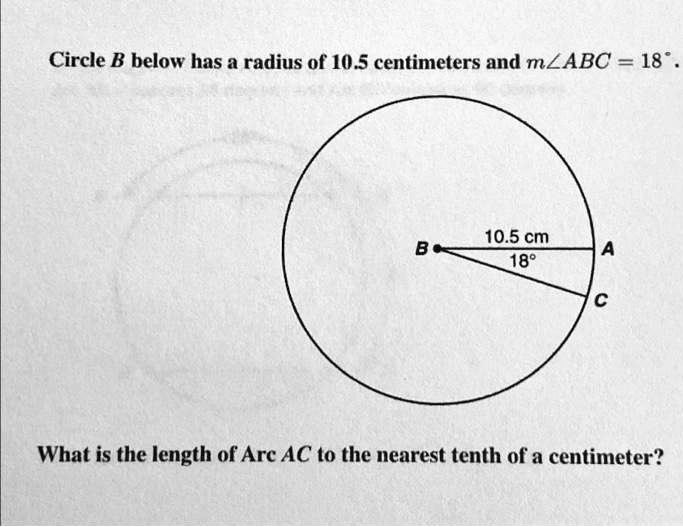
Circle B below has a radius of 10.5 centimeters and
. What is the length of Arc AC to the nearest tenth of a centimeter?
The Correct Answer and Explanation is:
To find the length of Arc AC in Circle B, we use the arc length formula:
Arc length=(θ360)×2πr\text{Arc length} = \left(\frac{\theta}{360}\right) \times 2\pi r
Given:
- Radius r=10.5r = 10.5 cm
- Central angle θ=18∘\theta = 18^\circ
Substitute the values into the formula:
Arc length=(18360)×2π×10.5\text{Arc length} = \left(\frac{18}{360}\right) \times 2\pi \times 10.5
=(120)×2π×10.5= \left(\frac{1}{20}\right) \times 2\pi \times 10.5
=21π20= \frac{21\pi}{20}
Using π≈3.1416\pi \approx 3.1416:
Arc length≈21×3.141620≈65.973620≈3.3 cm\text{Arc length} \approx \frac{21 \times 3.1416}{20} \approx \frac{65.9736}{20} \approx 3.3 \text{ cm}
Final Answer:
The length of Arc AC is approximately 3.3 centimeters.
Explanation
To determine the length of an arc in a circle, we rely on a fundamental geometric relationship that connects the arc length to the central angle and the radius. The arc length is a portion of the circle’s circumference, and its size depends on how large the central angle is compared to a full circle. A full circle has 360 degrees, so if the central angle is a fraction of that, the arc length is the same fraction of the total circumference.
In this problem, Circle B has a radius of 10.5 centimeters and a central angle of 18 degrees. The formula for arc length is:
Arc length=(θ360)×2πr\text{Arc length} = \left(\frac{\theta}{360}\right) \times 2\pi r
This formula calculates what fraction of the full circumference the arc represents. The term 2πr2\pi r gives the total circumference of the circle, and multiplying it by θ360\frac{\theta}{360} scales it down to the arc’s portion.
By substituting the given values into the formula, we find that the arc length is approximately 3.3 centimeters. This result makes sense because 18 degrees is a small angle, and the arc it subtends should be a small portion of the circle’s perimeter.
This type of calculation is not only useful in geometry but also in real-world applications such as engineering, architecture, and design. Whether you’re measuring the curved edge of a mechanical part or designing a circular track, understanding how to compute arc lengths is essential. It demonstrates how mathematical principles translate into practical tools for solving spatial problems.
