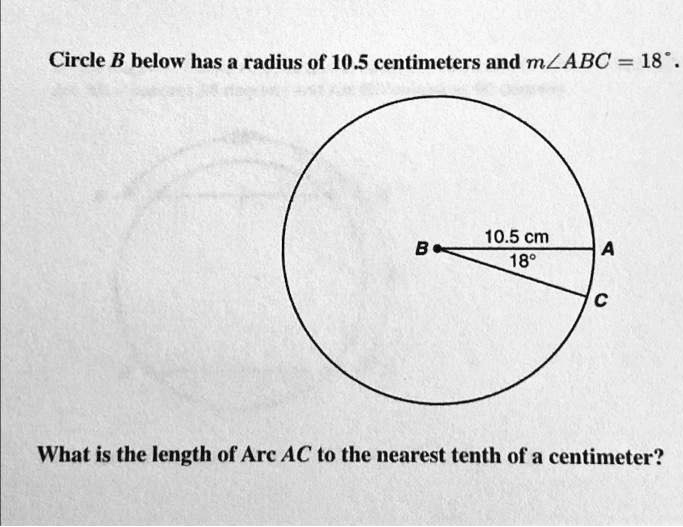
Circle B below has a radius of 10.5 centimeters and
. What is the length of Arc AC to the nearest tenth of a centimeter?
The Correct Answer and Explanation is:
To find the length of Arc AC, we can use the formula for the length of an arc in a circle: Arc Length=2πr×θ360\text{Arc Length} = 2\pi r \times \frac{\theta}{360}Arc Length=2πr×360θ
Where:
- rrr is the radius of the circle,
- θ\thetaθ is the central angle in degrees.
Given that the radius r=10.5 cmr = 10.5 \, \text{cm}r=10.5cm and the central angle θ=18∘\theta = 18^\circθ=18∘, we can plug these values into the formula.
- Calculate the total circumference of the circle first:
Circumference=2π×10.5=66 cm(approx.)\text{Circumference} = 2\pi \times 10.5 = 66 \, \text{cm} \quad (\text{approx.})Circumference=2π×10.5=66cm(approx.)
- Now calculate the fraction of the circle’s circumference that corresponds to the central angle of 18∘18^\circ18∘:
Arc Length=66×18360=66×0.05=3.3 cm\text{Arc Length} = 66 \times \frac{18}{360} = 66 \times 0.05 = 3.3 \, \text{cm}Arc Length=66×36018=66×0.05=3.3cm
Thus, the length of Arc AC to the nearest tenth of a centimeter is 3.3 cm.
