Use the alternative form of the derivative to find the derivative at x=c (if it exists)
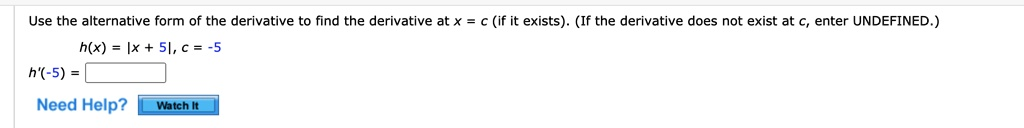
The Correct Answer and Explanation is:
We are given the function:h(x)=∣x+5∣,andc=−5h(x) = |x + 5|,\quad \text{and} \quad c = -5h(x)=∣x+5∣,andc=−5
We are asked to find the derivative at x=c=−5x = c = -5x=c=−5 using the alternative form of the derivative:h′(c)=limx→ch(x)−h(c)x−ch'(c) = \lim_{x \to c} \frac{h(x) – h(c)}{x – c}h′(c)=x→climx−ch(x)−h(c)
Let’s compute h(−5)h(-5)h(−5) first:h(−5)=∣−5+5∣=∣0∣=0h(-5) = |-5 + 5| = |0| = 0h(−5)=∣−5+5∣=∣0∣=0
Now substitute into the limit:h′(−5)=limx→−5∣x+5∣−0x+5=limx→−5∣x+5∣x+5h'(-5) = \lim_{x \to -5} \frac{|x + 5| – 0}{x + 5} = \lim_{x \to -5} \frac{|x + 5|}{x + 5}h′(−5)=x→−5limx+5∣x+5∣−0=x→−5limx+5∣x+5∣
To evaluate the limit, consider the behavior of the function as x→−5x \to -5x→−5 from the left and from the right.
From the left (x→−5−x \to -5^-x→−5−):
When x<−5x < -5x<−5, x+5<0x + 5 < 0x+5<0, so ∣x+5∣=−(x+5)|x + 5| = -(x + 5)∣x+5∣=−(x+5).
Thus,limx→−5−∣x+5∣x+5=limx→−5−−(x+5)x+5=−1\lim_{x \to -5^-} \frac{|x + 5|}{x + 5} = \lim_{x \to -5^-} \frac{-(x + 5)}{x + 5} = -1x→−5−limx+5∣x+5∣=x→−5−limx+5−(x+5)=−1
From the right (x→−5+x \to -5^+x→−5+):
When x>−5x > -5x>−5, x+5>0x + 5 > 0x+5>0, so ∣x+5∣=x+5|x + 5| = x + 5∣x+5∣=x+5.
Thus,limx→−5+∣x+5∣x+5=limx→−5+x+5x+5=1\lim_{x \to -5^+} \frac{|x + 5|}{x + 5} = \lim_{x \to -5^+} \frac{x + 5}{x + 5} = 1x→−5+limx+5∣x+5∣=x→−5+limx+5x+5=1
Since the left-hand limit is −1-1−1 and the right-hand limit is 111, the two-sided limit does not exist.
Therefore, the derivative at x=−5x = -5x=−5 does not exist.
✅ Final Answer:UNDEFINED\boxed{\text{UNDEFINED}}UNDEFINED
Explanation
The function h(x)=∣x+5∣h(x) = |x + 5|h(x)=∣x+5∣ is an absolute value function. Absolute value functions have sharp corners at points where the expression inside the absolute value equals zero. These corners are problematic because the function changes direction abruptly, and such sharp turns do not allow for a well-defined tangent line. In calculus, the derivative measures the slope of the tangent line at a point, and it only exists if the function is smooth — that is, if the limit from both sides agrees.
To find the derivative using the alternative form, we used the limit definition of the derivative:h′(c)=limx→ch(x)−h(c)x−ch'(c) = \lim_{x \to c} \frac{h(x) – h(c)}{x – c}h′(c)=x→climx−ch(x)−h(c)
We plugged in c=−5c = -5c=−5, and found that h(−5)=0h(-5) = 0h(−5)=0. Then the limit became:limx→−5∣x+5∣x+5\lim_{x \to -5} \frac{|x + 5|}{x + 5}x→−5limx+5∣x+5∣
This limit has different values depending on the direction from which xxx approaches −5-5−5. Approaching from the left gives −1-1−1, and from the right gives 111. Because these are not equal, the limit does not exist, and therefore the derivative is undefined.
This result makes sense because graphing h(x)=∣x+5∣h(x) = |x + 5|h(x)=∣x+5∣ shows a sharp corner at x=−5x = -5x=−5. At sharp corners, the slope changes instantaneously, so no single tangent line can be drawn — which means the derivative doesn’t exist at that point.
