The limit represents a derivative

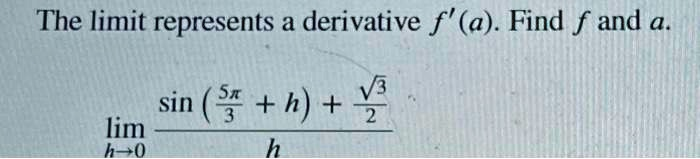
The Correct Answer and Explanation is:

To solve the given limit:

lim⁡h→0sin⁡(5π3+h)+32h\lim_{{h \to 0}} \frac{{\sin\left(\frac{5\pi}{3} + h\right) + \frac{\sqrt{3}}{2}}}{h}

we begin by comparing it to the standard definition of the derivative. The derivative of a function ff at a point aa is defined as:

f′(a)=lim⁡h→0f(a+h)−f(a)hf'(a) = \lim_{{h \to 0}} \frac{{f(a + h) – f(a)}}{h}

In the problem, the numerator is written with a plus sign instead of a subtraction. To reconcile this with the standard form, notice that:

sin⁡(5π3+h)+32=sin⁡(5π3+h)−(−32)\sin\left(\frac{5\pi}{3} + h\right) + \frac{\sqrt{3}}{2} = \sin\left(\frac{5\pi}{3} + h\right) – \left(-\frac{\sqrt{3}}{2}\right)

This suggests that f(x)=sin⁡(x)f(x) = \sin(x) and f(a)=−32f(a) = -\frac{\sqrt{3}}{2}. Since 5π3\frac{5\pi}{3} is the value being incremented by hh, we identify a=5π3a = \frac{5\pi}{3}. Evaluating f(a)f(a), we confirm:

f(5π3)=sin⁡(5π3)=−32f\left(\frac{5\pi}{3}\right) = \sin\left(\frac{5\pi}{3}\right) = -\frac{\sqrt{3}}{2}

Therefore, the expression inside the limit simplifies to the derivative of f(x)=sin⁡(x)f(x) = \sin(x) at a=5π3a = \frac{5\pi}{3}. The correct interpretation of the given limit is:

f(x)=sin⁡(x),a=5π3f(x) = \sin(x), \quad a = \frac{5\pi}{3}

The key to solving this problem lies in recognizing the structure of the difference quotient for derivatives and carefully matching the pieces of the given limit expression to the standard definition. This includes understanding trigonometric values and rephrasing the algebraic terms to fit the form f(a+h)−f(a)f(a + h) – f(a). Once aligned, the identity of ff and aa emerges naturally.