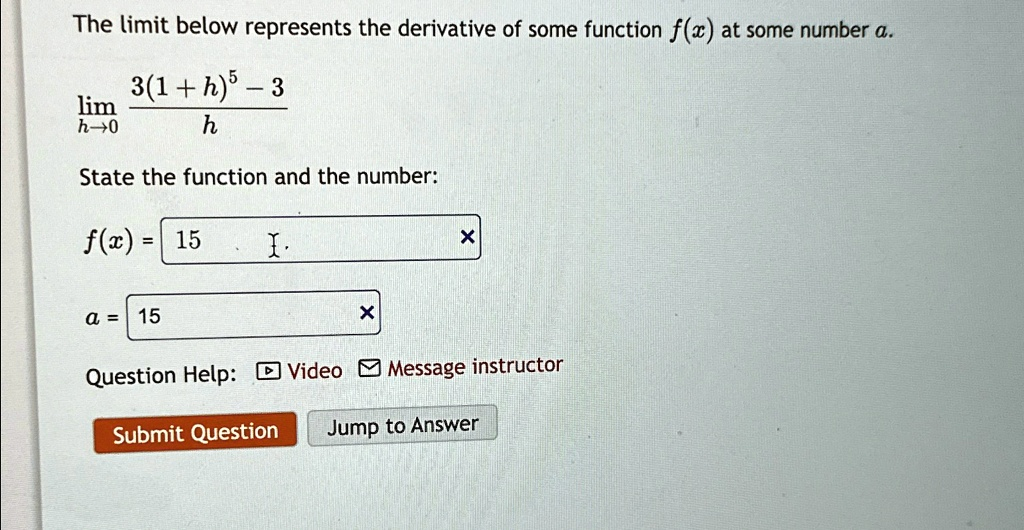
The Correct Answer and Explanation is:
The correct function is f(x)=3x5f(x) = 3x^5 and the number is a=1a = 1
Explanation:
The limit expression provided is:
limh→03(1+h)5−3h\lim_{h \to 0} \frac{3(1 + h)^5 – 3}{h}
This limit mirrors the standard definition of the derivative:
f′(a)=limh→0f(a+h)−f(a)hf'(a) = \lim_{h \to 0} \frac{f(a + h) – f(a)}{h}
To identify the function f(x)f(x) and the point aa, we analyze the structure of the expression. Notice that the numerator resembles a change in function value from f(a+h)f(a + h) to f(a)f(a), and it includes the factor 3(1+h)53(1 + h)^5. This suggests that the original function takes the form f(x)=3x5f(x) = 3x^5, since replacing xx with 1+h1 + h yields f(1+h)=3(1+h)5f(1 + h) = 3(1 + h)^5.
The expression subtracts 3 from this, indicating f(a)=3f(a) = 3. Using the function f(x)=3x5f(x) = 3x^5, we solve f(a)=3f(a) = 3 to find the value of aa. Setting:
3a5=3⇒a5=1⇒a=13a^5 = 3 \quad \Rightarrow \quad a^5 = 1 \quad \Rightarrow \quad a = 1
Therefore, the expression is the derivative of f(x)=3x5f(x) = 3x^5 evaluated at x=1x = 1.
This approach depends entirely on identifying the structure of the derivative definition. Once that structure is recognized, matching the limit expression allows for pinpointing both the original function and the evaluation point. Understanding this alignment is crucial to interpreting derivative limits correctly and builds a solid foundation for later applications in calculus.
