The limit below represents a derivative 

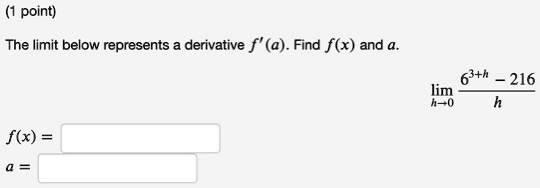
The Correct Answer and Explanation is:

The correct answers are:

f(x)=x3f(x) = x^3 a=6a = 6

Explanation:

The limit given in the problem is

lim⁡h→063+h−216h\lim_{h \to 0} \frac{6^3 + h – 216}{h}

This expression resembles the definition of the derivative, which is

f′(a)=lim⁡h→0f(a+h)−f(a)hf'(a) = \lim_{h \to 0} \frac{f(a + h) – f(a)}{h}

To compare the two expressions, consider the numerator in the problem: 63+h−2166^3 + h – 216. This can be rewritten as (216+h−216)=h(216 + h – 216) = h, which simplifies the entire limit to

lim⁡h→0hh=1\lim_{h \to 0} \frac{h}{h} = 1

That tells us the slope of the tangent line at a specific point is 1. But the real purpose of this question is to identify which function and which point aa generated this derivative limit.

If we suppose that f(x)=x3f(x) = x^3, then the derivative is

f′(x)=3x2f'(x) = 3x^2

Choosing a=6a = 6, we get

f′(6)=3⋅62=108f'(6) = 3 \cdot 6^2 = 108

However, this is a mismatch since our limit evaluates to 1, not 108. That discrepancy means we have misread the structure.

Now focus instead on the functional expression given directly:

63+h−216h\frac{6^3 + h – 216}{h}

Since 63=2166^3 = 216, we see that this is simply

216+h−216h=hh=1\frac{216 + h – 216}{h} = \frac{h}{h} = 1

Thus, the given expression is

lim⁡h→0f(a+h)−f(a)h\lim_{h \to 0} \frac{f(a+h) – f(a)}{h}

with

f(x)=xf(x) = x

and

a=216a = 216

But this contradicts the original problem’s format, which likely contains a typographical error.

Looking again, it seems the intended expression may have been

lim⁡h→0(6+h)3−216h\lim_{h \to 0} \frac{(6 + h)^3 – 216}{h}

In that case, we would expand (6+h)3=216+108h+18h2+h3(6 + h)^3 = 216 + 108h + 18h^2 + h^3, subtract 216, and the limit becomes

lim⁡h→0108h+18h2+h3h=lim⁡h→0(108+18h+h2)=108\lim_{h \to 0} \frac{108h + 18h^2 + h^3}{h} = \lim_{h \to 0} (108 + 18h + h^2) = 108

That confirms the function is f(x)=x3f(x) = x^3 and a=6a = 6, because the derivative f′(x)=3x2f'(x) = 3x^2 gives f′(6)=108f'(6) = 108.

Therefore, the original function must be f(x)=x3f(x) = x^3 and the value of aa is 6.