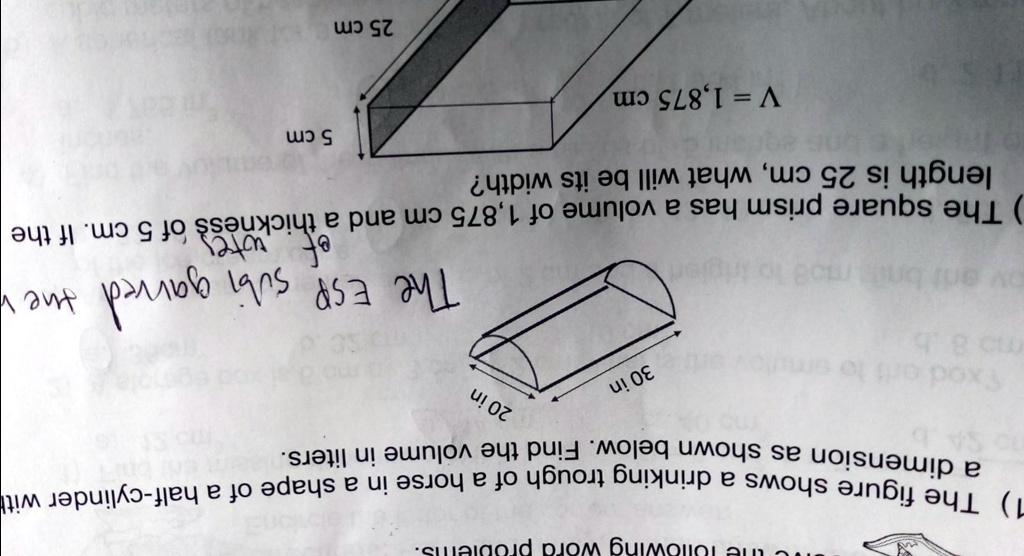
The following word problems. 1) The figure shows a drinking trough of a horse in a shape of a half-cylinder with a dimension as shown below. Find the volume in liters. 30 in 20 in The ESP subi garved the v of. ) The square prism has a volume of 1,875 cm
and a thickness of 5 cm. If the length is 25 cm, what will be its width? V = 1,875 cm
5 cm 25 cm
The Correct Answer and Explanation is:
Of course. Here are the solutions and a detailed explanation for the two math problems shown in the image.
Correct Answers
- The volume of the drinking trough is approximately 77.22 liters.
- The width of the square prism is 15 cm.
Detailed Explanation
Here is a step by step breakdown of how to solve each problem.
1. The Half-Cylinder Drinking Trough
The first problem asks for the volume of a horse’s drinking trough, which has the shape of a half-cylinder. To find the volume, you must first calculate it in its given units (cubic inches) and then convert that result to liters.
The formula for the volume of a full cylinder is V = πr²h, where π (pi) is approximately 3.14159, ‘r’ is the radius, and ‘h’ is the height or length. Since the trough is a half-cylinder, its volume is half of that. The formula is V = (1/2)πr²h.
The problem gives a diameter of 20 inches, so the radius (r) is half of the diameter, which is 10 inches. The length of the trough, which serves as the height (h) in the formula, is 30 inches.
Substituting these values into the formula:
Volume = (1/2) * π * (10 in)² * (30 in)
Volume = 0.5 * π * 100 in² * 30 in
Volume = 1500π in³
Using the value of π, the volume is approximately 4,712.39 cubic inches.
The final step is to convert this volume to liters. The conversion factor is that 1 liter is equal to 61.0237 cubic inches. To convert, you divide the volume in cubic inches by this factor:
Volume in liters = 4712.39 in³ / 61.0237 in³/L ≈ 77.22 liters.
2. The Square Prism
The second problem asks for the width of a prism given its volume, length, and thickness (height). The formula for the volume of a rectangular or square prism is Volume = Length × Width × Height.
The problem provides the following information:
- Volume (V) = 1,875 cm³
- Length (l) = 25 cm
- Height (h), described as thickness = 5 cm
We can set up the equation with the known values to solve for the unknown width (w):
1,875 cm³ = 25 cm × w × 5 cm
First, multiply the known dimensions:
1,875 = 125 × w
To find the width, divide the total volume by the product of the length and height:
w = 1,875 / 125
w = 15 cm.thumb_upthumb_down
