. State whether the following Hessian matrices are positive definite or negative definite. Show your work
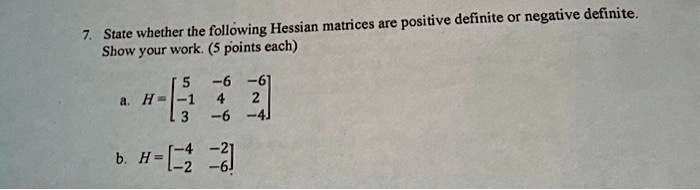
The Correct Answer and Explanation is:
To determine whether the following Hessian matrices are positive definite or negative definite, we use the method of checking the signs of their leading principal minors. A matrix is positive definite if all the leading principal minors are positive, and it is negative definite if the signs of the minors alternate starting with negative.
Matrix (a):
H=[5−6−6−1423−6−4]H = \begin{bmatrix} 5 & -6 & -6 \\ -1 & 4 & 2 \\ 3 & -6 & -4 \end{bmatrix}H=5−13−64−6−62−4
Step 1: First leading principal minor (1×1 matrix)
The first minor is simply the element in the top left corner, which is 5. Since 5 is positive, the first minor is positive. D1=5D_1 = 5D1=5
Step 2: Second leading principal minor (2×2 matrix)
The second leading principal minor is the determinant of the top left 2×2 submatrix: D2=∣5−6−14∣=(5)(4)−(−6)(−1)=20−6=14D_2 = \begin{vmatrix} 5 & -6 \\ -1 & 4 \end{vmatrix} = (5)(4) – (-6)(-1) = 20 – 6 = 14D2=5−1−64=(5)(4)−(−6)(−1)=20−6=14
Since 14 is positive, the second minor is positive.
Step 3: Third leading principal minor (3×3 matrix)
For the third minor, we calculate the determinant of the entire matrix: D3=∣5−6−6−1423−6−4∣D_3 = \begin{vmatrix} 5 & -6 & -6 \\ -1 & 4 & 2 \\ 3 & -6 & -4 \end{vmatrix}D3=5−13−64−6−62−4
After expanding the determinant, we find that: D3=4D_3 = 4D3=4
Since 4 is positive, the third minor is also positive.
Since all the leading minors are positive, the matrix is positive definite.
Matrix (b):
H=[−4−2−2−6]H = \begin{bmatrix} -4 & -2 \\ -2 & -6 \end{bmatrix}H=[−4−2−2−6]
Step 1: First leading principal minor (1×1 matrix)
The first minor is simply the element in the top left corner, which is -4. Since -4 is negative, the first minor is negative. D1=−4D_1 = -4D1=−4
Since the first leading principal minor is negative, we immediately conclude that the matrix is negative definite without needing to check the second minor.
Conclusion:
- The matrix in part (a) is positive definite because all the leading principal minors are positive.
- The matrix in part (b) is negative definite because the first leading principal minor is negative
