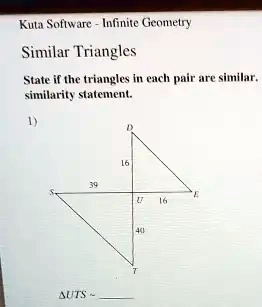
Kuta Software – Infinite Geometry Similar Triangles State if the triangles in each pair are similar. similarity statement. 1) D 16 39 E U 16 40 T \triangle UTS \sim
The Correct Answer and Explanation is:
The triangles are not similar.
Similarity Statement: ΔUTS ∼ not similar
Explanation
To determine whether two triangles are similar, we must verify if their corresponding sides are proportional or if their corresponding angles are congruent. In this problem, we are given two triangles: ΔDUE and ΔUTS. The side lengths provided are:
- DU = 16
- UE = 16
- UT = 40
- TS = 39
We are asked to determine if ΔUTS is similar to another triangle, presumably ΔDUE, based on the given side lengths. Since no angles are provided, we rely on the Side-Side-Side (SSS) similarity criterion, which states that if the ratios of all three pairs of corresponding sides are equal, then the triangles are similar.
Let us compare the corresponding sides:
- DU corresponds to UT: DU / UT = 16 / 40 = 2 / 5
- UE corresponds to TS: UE / TS = 16 / 39
Now we compare the two ratios:
- 2 / 5 = 0.4
- 16 / 39 ≈ 0.410
These values are not equal. Even a small difference in ratios means the triangles are not similar under the SSS criterion. Since the side ratios do not match, we cannot conclude similarity based on proportional sides.
Additionally, no information is given about the angles, so we cannot apply the Angle-Angle (AA) or Side-Angle-Side (SAS) similarity criteria either.
This problem illustrates the importance of precise proportionality when determining triangle similarity. Even if two triangles appear visually similar, they must meet strict mathematical conditions to be classified as similar. Understanding these criteria is essential in geometry, especially when solving problems involving scale, indirect measurement, or geometric proofs.
