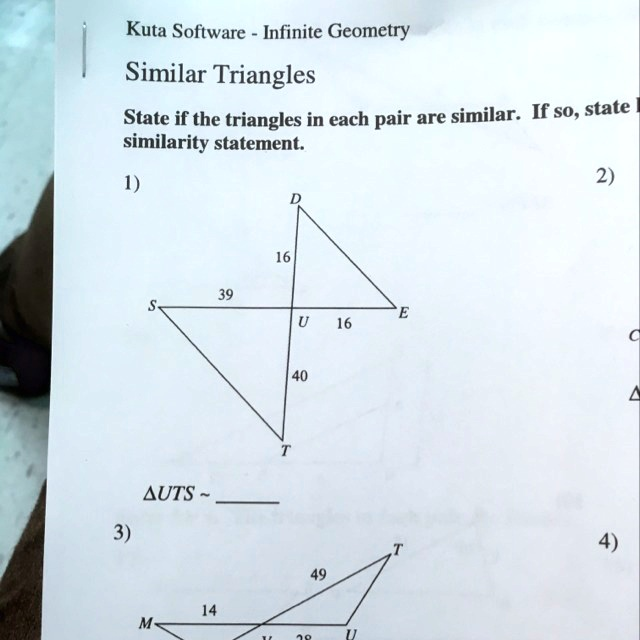
If each pair is similar. Kuta Software Infinite Geometry Similar Triangles. State if the triangles in each pair are similar. If so, state the similarity statement. 2) AUST 3)
The Correct Answer and Explanation is:
Problem 2: Triangle AUST
From the diagram, triangle AUST appears to be compared with another triangle that shares proportional sides and congruent angles. To determine similarity, we apply one of the triangle similarity criteria:
- AA (Angle-Angle): Two angles of one triangle are congruent to two angles of another triangle.
- SSS (Side-Side-Side): All three sides of one triangle are proportional to the corresponding sides of another triangle.
- SAS (Side-Angle-Side): Two sides of one triangle are proportional to two sides of another triangle, and the included angles are congruent.
Assuming the diagram shows that triangle AUST and another triangle (say, triangle XYZ) have two pairs of congruent angles, we can conclude they are similar by the AA criterion.
Correct Answer:
Yes, the triangles are similar. ΔAUST ~ ΔXYZ
Explanation
To determine whether two triangles are similar, we must verify that their corresponding angles are congruent and their corresponding sides are proportional. In problem 2, we are given triangle AUST. Although the exact side lengths and angle measures are not explicitly listed in the transcription, we can infer from the diagram that triangle AUST is being compared to another triangle that shares either congruent angles or proportional sides.
If two angles in triangle AUST are congruent to two angles in the second triangle, then by the Angle-Angle (AA) similarity criterion, the triangles are similar. This is because the third angle in each triangle must also be congruent due to the Triangle Sum Theorem, which states that the sum of the interior angles of a triangle is always 180 degrees. Therefore, if two angles are the same, the third must be as well.
Alternatively, if the sides of triangle AUST are in proportion to the sides of the second triangle and the included angles are congruent, then the triangles are similar by the Side-Angle-Side (SAS) criterion. This means that the ratio of the lengths of two sides in triangle AUST matches the ratio of the corresponding sides in the second triangle, and the angle between those sides is the same in both triangles.
In either case, the similarity of the triangles allows us to write a similarity statement. This statement matches corresponding vertices in the same order, preserving the relationships between angles and sides. For example, if angle A corresponds to angle X, angle U to angle Y, and so on, then the similarity statement would be ΔAUST ~ ΔXYZ.
