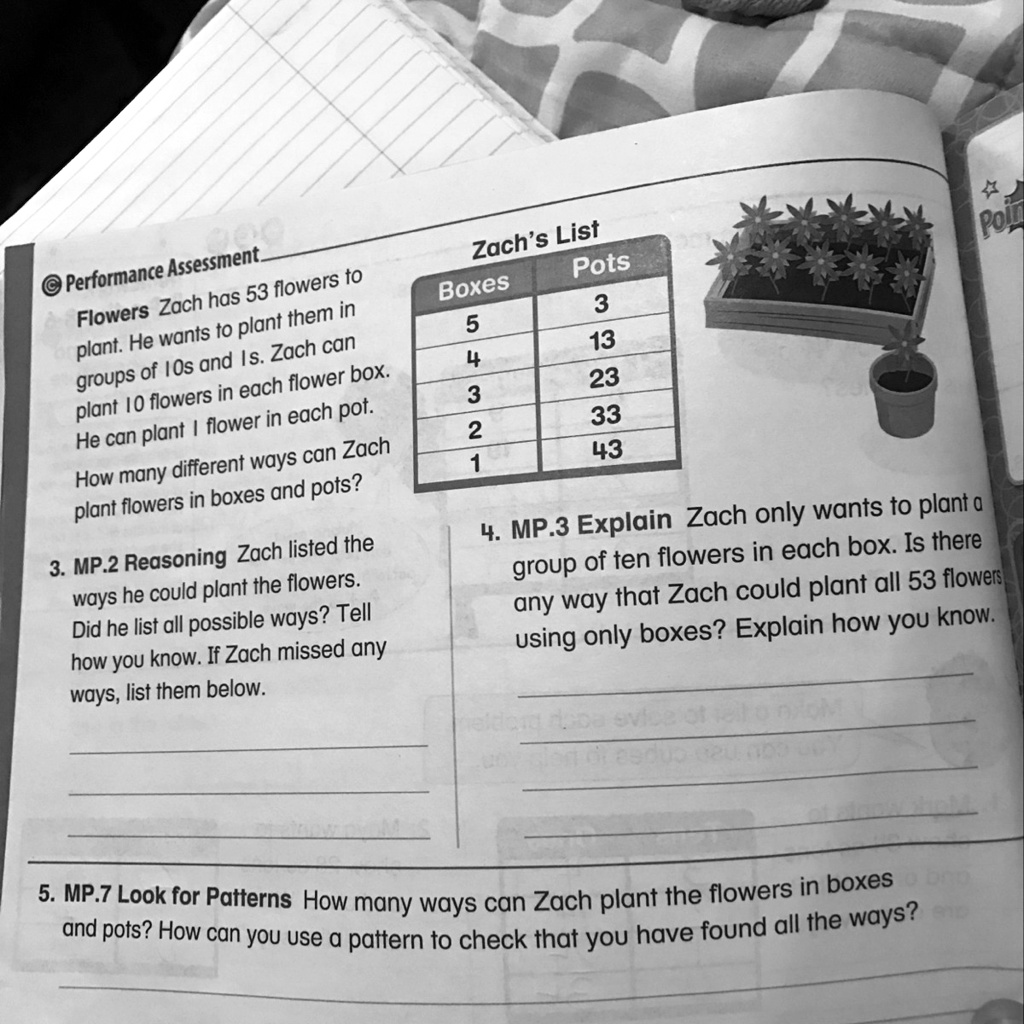
Performance Assessment Zach’s List Flowers Zach has 53 flowers to plant. He wants to plant them in Boxes Pots groups of 10s and Is. Zach can 5 3 plant 10 flowers in each flower box. 4 13 He can plant I flower in each pot. 3 23 How many different ways can Zach 2 33 plant flowers in boxes and pots? 1 43 3. MP.2 Reasoning Zach listed the ways he could plant the flowers. Did he list all possible ways? Tell how you know. If Zach missed any ways, list them below. 4. MP.3 Explain Zach only wants to plant a group of ten flowers in each box. Is there any way that Zach could plant all 53 flowers using only boxes? Explain how you know. 5. MP.7 Look for Patterns How many ways can Zach plant the flowers in boxes and pots? How can you use a pattern to check that you have found all the ways
The Correct Answer and Explanation is:
Total Number of Flowers:
Zach has 53 flowers.
Boxes and Pots:
- Each box holds 10 flowers.
- Each pot holds 1 flower.
Zach is trying to find all the combinations of boxes and pots that add up to 53 flowers, where the number of flowers from boxes is a multiple of 10. That is, for any number of boxes xx, the total from boxes is 10x10x, and the remaining flowers, 53−10×53 – 10x, go into pots.
Let’s list all possible values of xx for which 10x≤5310x \leq 53:
| Boxes (x) | Pots (53 – 10x) |
|---|---|
| 0 | 53 |
| 1 | 43 |
| 2 | 33 |
| 3 | 23 |
| 4 | 13 |
| 5 | 3 |
These are all the possible combinations because 6 boxes would require 60 flowers, which exceeds 53.
Answer to MP.2 Reasoning:
Yes, Zach missed one way:
- 0 boxes and 53 pots.
He listed combinations starting from 1 box, but we must include 0 boxes as a valid choice since 0 is a whole number and allowed in this context.
Answer to MP.3 Explanation:
No, Zach cannot plant all 53 flowers using only boxes. Each box holds 10 flowers, so only multiples of 10 are possible: 10, 20, 30, 40, 50, 60… Since 53 is not a multiple of 10, it’s impossible to use only boxes.
Answer to MP.7 Pattern Observation:
There are 6 total ways Zach can plant the flowers using boxes and pots, from 0 to 5 boxes.
A pattern appears:
- For each increase of 1 box, you remove 10 from the number of pots. So the sequence is: (0,53), (1,43), (2,33), (3,23), (4,13), (5,3) — decreasing pots by 10 each time.
This pattern confirms all combinations are found and follows a clear, predictable rule.
