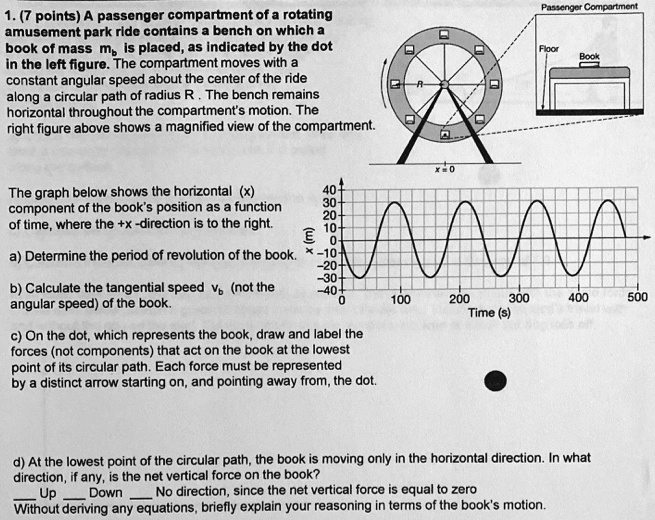
passenger compartment of a rotating amusement park ride contains a bench on which a book of mass Mp is placed; as indicated by the dot in the left figure. The compartment moves with a constant angular speed about the center of the ride along a circular path of radius R. The bench remains horizontal throughout the compartment’s motion. The right figure above shows a magnified view of the compartment. The graph below shows the horizontal component of the book’s position as a function of time, where the +x-direction is to the right: E a) Determine the period of revolution of the book. b) Calculate the tangential speed (angular speed) of the book. c) On the dot, which represents the book, draw and label the forces (not components) that act on the book at the lowest point of its circular path. Each force must be represented by a distinct arrow starting on and pointing away from the dot. d) At the lowest point of the circular path, the book is moving only in the horizontal direction. In what direction, if any, is the net vertical force on the book? Down. No direction, since the net vertical force is equal to zero. Without deriving any equations, briefly explain your reasoning in terms of the book’s motion.
The Correct Answer and Explanation is:
Here are the solutions to the physics problem:
a) Determine the period of revolution of the book.
The period of revolution is T = 100 s.
b) Calculate the tangential speed v_b of the book.
The tangential speed is v_b = 0.6π m/s (approximately 1.88 m/s).
c) On the dot, which represents the book, draw and label the forces…
The free-body diagram for the book at its lowest point has two forces acting on it:
- Gravitational force (F_g or Weight): An arrow pointing vertically downward from the dot.
- Normal force (F_N): An arrow pointing vertically upward from the dot.
The arrow representing the normal force (F_N) must be drawn longer than the arrow representing the gravitational force (F_g).
d) At the lowest point of the circular path… in what direction, if any, is the net vertical force on the book?
The net vertical force is directed Up.
Explanation
This problem involves the principles of uniform circular motion. Here is a step-by-step explanation for each part of the solution.
a) Period of Revolution:
The period (T) is the time it takes for an object to complete one full cycle of its motion. The provided graph plots the book’s horizontal position (x) against time (t). We can find the period by identifying the time interval for one complete wave. For example, the graph shows a peak (maximum positive displacement) at t = 75 s and the next peak at t = 175 s. The time elapsed between these two consecutive peaks is the period:
T = 175 s – 75 s = 100 s.
b) Tangential Speed:
The tangential speed (v_b) for an object moving in a circle is calculated with the formula v_b = 2πR/T, where R is the radius of the circle and T is the period. The radius of the ride’s path corresponds to the amplitude of the horizontal motion shown in the graph. The maximum value of x is 30 m, so the radius R = 30 m. Using the period T = 100 s found in part (a), we can calculate the speed:
v_b = (2 * π * 30 m) / 100 s = 60π / 100 m/s = 0.6π m/s.
c) Free-Body Diagram at the Lowest Point:
At the lowest point of its path, two main forces act on the book. The Earth’s gravity pulls the book downward (F_g), and the bench pushes upward with a normal force (F_N). Because the book is moving along a circular path, there must be a net force, called the centripetal force, directed toward the center of the circle. At the bottom of the ride, the center of the circle is directly above the book. This means the net force must be directed upward. For the net force to be upward, the magnitude of the upward normal force must be greater than the magnitude of the downward gravitational force (F_N > F_g).
d) Direction of Net Vertical Force:
The net vertical force on the book is directed Up. An object moving in a circle is continuously accelerating because the direction of its velocity is always changing. This acceleration, known as centripetal acceleration, always points towards the center of the circular path. According to Newton’s second law of motion (F_net = ma), an acceleration is caused by a net force that acts in the same direction. At the lowest point of the circular path, the center of the circle is vertically above the book. Therefore, the book’s acceleration is upward, and the net force causing this acceleration must also be directed upward.
