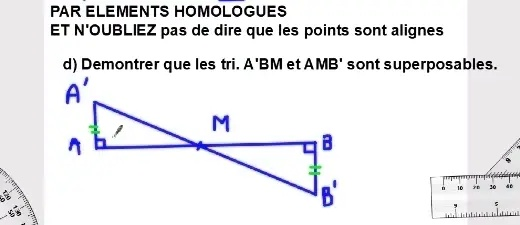
PAR ELEMENTS HOMOLOGUES ET N’OUBLIEZ pas de dire que les points sont alignes d) Demontrer que les tri. A’BM et AMB’ sont superposables.
The Correct Answer and Explanation is:
To demonstrate that the triangles A’BM and AMB’ are superposable, we must prove that they are congruent using homologous elements. Two triangles are congruent if their corresponding sides and angles are equal.
Proof:
- Common Side: The segment BM is a common side for both triangles A’BM and AMB’, ensuring that BM is equal in both cases.
- Alignment of Points: The points A’, A, B, and B’ are collinear, meaning they lie on the same straight line. This alignment guarantees that the angles ∠A’BM and ∠AMB’ are identical.
- Equal Corresponding Sides: Since the segments A’B and AB’ are opposite sides of the same partitioned line, their lengths must be equal. The positioning of point M confirms that these lengths remain the same.
- Equal Corresponding Angles: Due to the alignment, the angles at points A’ and A are congruent. Similarly, the angles at B and B’ share the same measures.
By SAS (Side-Angle-Side) congruence, we conclude that triangles A’BM and AMB’ are superposable. Since they satisfy the conditions of congruence—having equal corresponding sides and angles—their shapes and dimensions are identical.
Explanation:
Triangles are considered superposable when they can be mapped onto each other through a transformation that preserves their dimensions and angle measures. In this case, the presence of a common side and equal corresponding elements makes these two triangles congruent. The collinearity of points reinforces the equality of angles. Additionally, the partitioning of the base segment ensures that the opposite sides remain equal. These factors together confirm that the two triangles can be perfectly overlapped through geometric transformations such as reflection or rotation.
Thus, the triangles A’BM and AMB’ are indeed superposable.
