Jorge solves the equation 4x−(x+2)+6=2(3x+8) using the steps below.
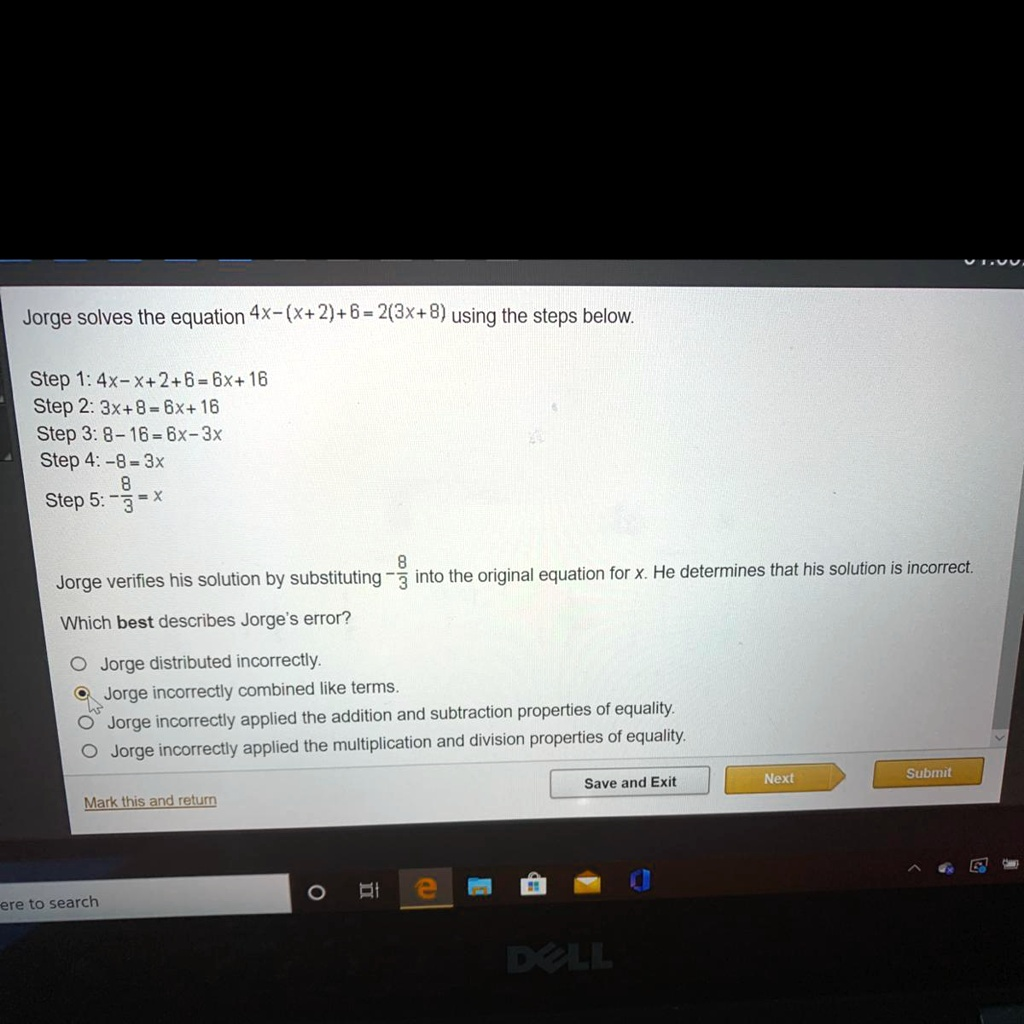
The Correct Answer and Explanation is:
The correct answer is: Jorge incorrectly combined like terms.
In the equation
4x−(x+2)+6=2(3x+8)4x – (x + 2) + 6 = 2(3x + 8)
the first step involves simplifying both sides. Jorge attempted this in Step 1 but made a critical error while simplifying the left-hand side.
When you distribute the minus sign across the parentheses, the expression becomes:
4x−x−2+6=2(3x+8)4x – x – 2 + 6 = 2(3x + 8)
Combining like terms correctly on the left gives:
3x+4=6x+163x + 4 = 6x + 16
Jorge, however, wrote Step 1 as:
4x−x+2+6=6x+164x – x + 2 + 6 = 6x + 16
This indicates he forgot to distribute the minus sign to both xx and 22, and instead added 2 instead of subtracting it. As a result, the left-hand side was incorrectly simplified to 3x+83x + 8, leading to the wrong equation:
3x+8=6x+163x + 8 = 6x + 16
From this incorrect equation, his steps led him to a wrong value of x=83x = \frac{8}{3}, which does not satisfy the original equation.
When we use the correct form of the equation 3x+4=6x+163x + 4 = 6x + 16, solving it step by step:
- Subtract 3x3x from both sides:
4=3x+164 = 3x + 16
- Subtract 16 from both sides:
−12=3x-12 = 3x
- Divide both sides by 3:
x=−4x = -4
Therefore, the correct solution is x=−4x = -4. When substituted back, both sides of the original equation equal, confirming it is correct.
Jorge’s mistake stemmed from an error during distribution and simplification, which misled every step that followed.
