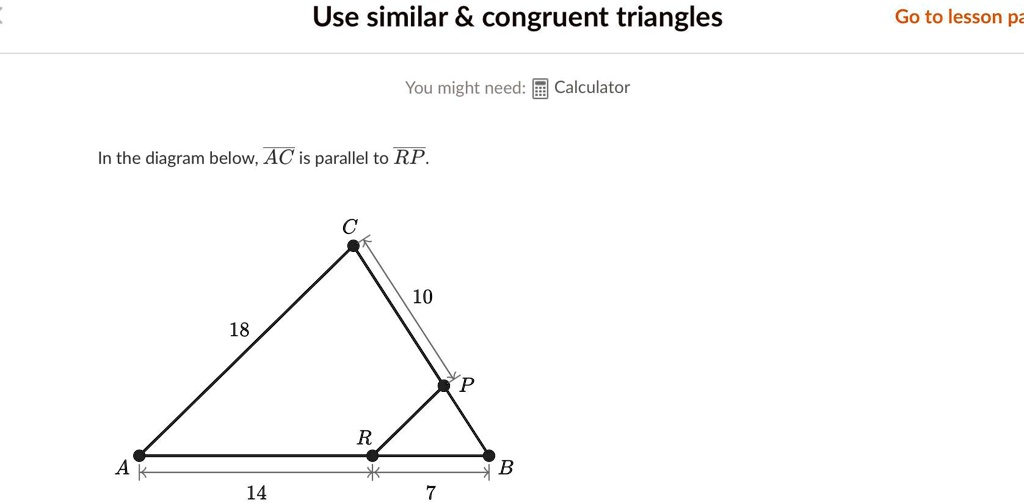
Use similar & congruent triangles You might need: Calculator In the diagram below, \overline{AC} is parallel to \overline{RP}.
The Correct Answer and Explanation is:
To solve the problem, we begin by using triangle similarity. Given that AC is parallel to RP, triangle ABC and triangle RBP share corresponding angles formed by a transversal intersecting parallel lines. This implies that △ABC ∼ △PRB by the Angle-Angle (AA) similarity criterion.
From the diagram, we know:
- AB = 14 units
- RB = 7 units
- AC = 18 units
- CP = 10 units
Since RB is part of AB, triangle ARB is a smaller triangle within △ABC, and triangle PRC is created by connecting point P on BC with point R on AB, forming triangle PRC with the parallel segment RP.
Using the similarity from the parallel lines:
ABRB=ACPC\frac{AB}{RB} = \frac{AC}{PC}
Substitute the known values:
147=18x\frac{14}{7} = \frac{18}{x}
Simplify the left-hand side:
2=18×2 = \frac{18}{x}
Now solve for x:
x=182=9x = \frac{18}{2} = 9
Thus, the length of segment PC is 9 units.
Explanation:
The key idea here lies in the parallel segments AC and RP. When a line segment is drawn between two sides of a triangle and is parallel to the third side, it creates a smaller triangle that is similar to the original triangle. This means that all corresponding sides of the two triangles are in proportion.
In triangle ABC, when RP is drawn parallel to AC, we can say triangle RBP ∼ triangle ABC. Because similarity preserves the ratio of side lengths, we can create proportions using corresponding sides. Once we identify these ratios and substitute the known values, we use simple algebra to find the missing length.
This method efficiently uses the properties of similar triangles and proportionality to find unknown lengths, a foundational concept in geometric reasoning.
