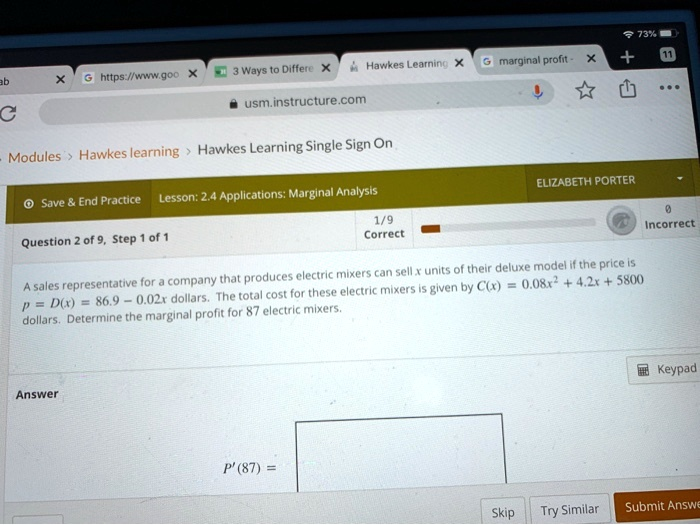
Hawkes Learning Marginal profit = G https://lnwgoo Ways Different usm.instructure.com Hawkes Learning Single Sign On Modules Hawkes Learning ELIZABETH PORTER Lesson: 2.4 Applications: Marginal Analysis 0 Save End Practice 1/9 of 9, Step of 1 Correct Question Incorrect The company sells units of their deluxe model. If the price set by the company that produces electric mixers is represented by p(x) = 0.0812x + 425, where x is the number of electric mixers sold, and the total cost for these electric mixers is given by C(x) = 86.9 + 0.02x dollars, determine the marginal profit for 87 electric mixers. Answer: p'(87) = Skip Try Similar Submit Answer
The Correct Answer and Explanation is:
To find the marginal profit at a production level of 87 mixers, we need to understand that marginal profit is defined as the derivative of the profit function, evaluated at a given value of xx. That is,
P′(x)=R′(x)−C′(x)P'(x) = R'(x) – C'(x)
where
- R(x)R(x) is the revenue function, defined as R(x)=x⋅p(x)R(x) = x \cdot p(x),
- C(x)C(x) is the cost function,
- p(x)=0.0812x+425p(x) = 0.0812x + 425, and
- C(x)=86.9+0.02xC(x) = 86.9 + 0.02x.
Step 1: Find the revenue function R(x)R(x)
Since revenue is price times quantity,
R(x)=x⋅p(x)=x(0.0812x+425)=0.0812×2+425x.R(x) = x \cdot p(x) = x(0.0812x + 425) = 0.0812x^2 + 425x.
Step 2: Differentiate the revenue and cost functions
Differentiating R(x)R(x):
R′(x)=ddx[0.0812×2+425x]=2⋅0.0812x+425=0.1624x+425.R'(x) = \frac{d}{dx}[0.0812x^2 + 425x] = 2 \cdot 0.0812x + 425 = 0.1624x + 425.
Differentiating C(x)C(x):
C′(x)=ddx[86.9+0.02x]=0.02.C'(x) = \frac{d}{dx}[86.9 + 0.02x] = 0.02.
Step 3: Compute marginal profit at x=87x = 87
P′(87)=R′(87)−C′(87)=(0.1624⋅87+425)−0.02.P'(87) = R'(87) – C'(87) = (0.1624 \cdot 87 + 425) – 0.02.
P′(87)=(14.1288+425)−0.02=439.1288−0.02=439.1088.P'(87) = (14.1288 + 425) – 0.02 = 439.1288 – 0.02 = 439.1088.
Final Answer:
P′(87)=439.1088\boxed{P'(87) = 439.1088}
This value represents the approximate additional profit earned by producing and selling one more electric mixer after 87 units. Marginal analysis like this helps companies determine the efficiency of scaling production and optimizing output. Since profit increases by approximately 439.11 dollars for the 88th mixer, it may be advantageous to produce it assuming demand and other conditions remain stable.
