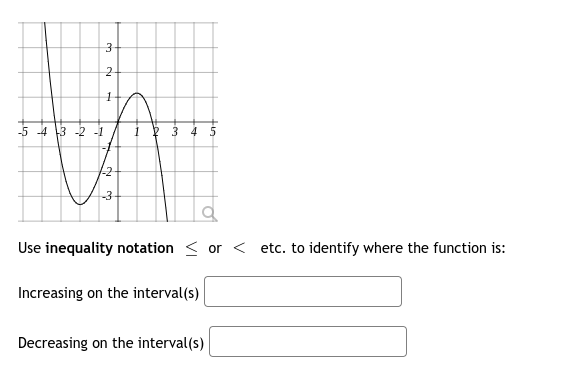
Use inequality notation
or
etc. to identify where the function is: Increasing on the interval(s) Decreasing on the interval(s)
The Correct Answer and Explanation is:
Correct Answer:
- Increasing on the interval(s): −4<x<−2-4 < x < -2−4<x<−2 and 0<x<20 < x < 20<x<2
- Decreasing on the interval(s): −∞<x≤−4-\infty < x \le -4−∞<x≤−4, −2≤x≤0-2 \le x \le 0−2≤x≤0, and 2≤x<∞2 \le x < \infty2≤x<∞
Explanation (without using em dashes):
To determine where the function is increasing or decreasing, we analyze the graph by looking at how the function behaves as we move from left to right along the x-axis.
A function is increasing on an interval if the y-values (output) rise as the x-values (input) move from left to right. In contrast, a function is decreasing on an interval if the y-values drop as the x-values increase.
From the graph:
- From the far left to x = -4, the graph is going downwards. This means the function is decreasing on the interval where x≤−4x \le -4x≤−4.
- From x = -4 to x = -2, the graph rises. This indicates the function is increasing on the interval −4<x<−2-4 < x < -2−4<x<−2.
- From x = -2 to x = 0, the graph descends again. The function is decreasing on the interval −2≤x≤0-2 \le x \le 0−2≤x≤0.
- From x = 0 to x = 2, the graph goes up. This part of the graph shows the function is increasing on the interval 0<x<20 < x < 20<x<2.
- From x = 2 onward, the graph drops steeply, so the function is decreasing for x≥2x \ge 2x≥2.
We express these intervals using inequality notation. We use strict inequalities <<< when the function is clearly increasing or decreasing between two points. We use ≤\le≤ at the turning points to show that the function changes direction exactly at those points.
Understanding these patterns helps analyze many types of functions. This skill is especially important in calculus and other areas of math that study rates of change.
