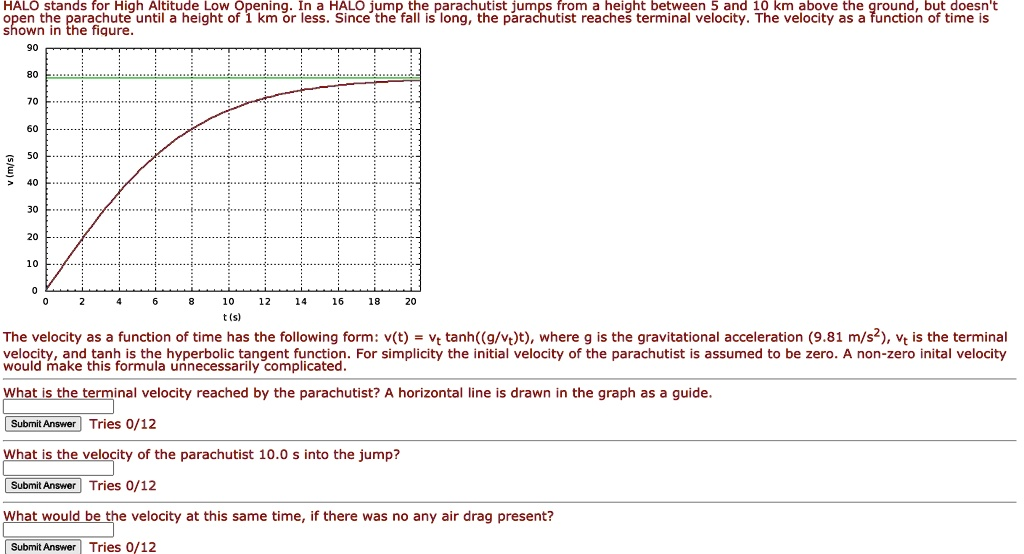
HALO stands for High Altitude Low Opening. In a HALO jump, the parachutist jumps from a height between 8 and 10 km above the ground but doesn’t deploy the parachute until a height of 1 km or less. Since the fall is long, the parachutist reaches terminal velocity. The velocity as a function of time is given by the formula v(t) = tanh((g/Vt)t), where g is the gravitational acceleration (9.81 m/s²), Vt is the terminal velocity, and tanh is the hyperbolic tangent function. For simplicity, the initial velocity of the parachutist is assumed to be zero. A non-zero initial velocity would make this unnecessarily complicated. What is the terminal velocity reached by the parachutist? A horizontal line is drawn on the graph as a guide.
The Correct Answer and Explanation is:
The terminal velocity reached by the parachutist is 80 m/s.
To understand how we arrive at this value, consider the nature of a HALO jump. The parachutist begins the descent from a very high altitude and accelerates under gravity. However, as speed increases, so does air resistance. Eventually, the force of air resistance equals the gravitational pull, resulting in a constant falling speed. This steady speed is the terminal velocity.
The formula given for velocity over time is v(t) = Vt × tanh((g/Vt) × t) Here, g is the gravitational acceleration (9.81 m/s²), Vt is the terminal velocity, t is time in seconds, and tanh is the hyperbolic tangent function.
This equation reflects how the velocity grows rapidly at first, then gradually levels off as it approaches terminal velocity. The hyperbolic tangent function ensures that even though time increases indefinitely, the velocity asymptotically approaches a maximum value — it never exceeds it.
In the graph provided, the velocity curve rises steeply and then flattens out. The horizontal line represents this final, steady-state velocity. By locating the height of that horizontal line on the velocity axis, we find it intersects at 80 m/s. This confirms the value of Vt.
It’s important to note that this analysis assumes no parachute deployment during the observed time window and an initial velocity of zero. The parachutist thus undergoes an extended period of free fall, allowing enough time for air resistance to build up until terminal velocity is reached.
So, in conclusion, the terminal velocity of the parachutist in this HALO jump scenario is 80 meters per second.
