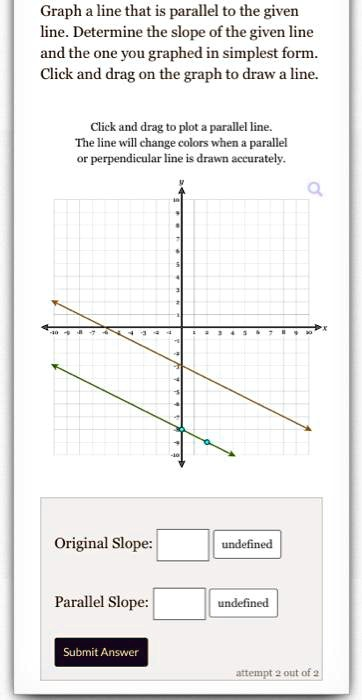
Graph a line that is parallel to the given line. Determine the slope of the given line and the one you graphed in simplest form. Click and drag on the graph to draw the line. Click and drag to plot a parallel line. The line will change color when parallel and perpendicular lines are accurately drawn. Original Slope: underlined Parallel Slope: underlined Submit Answer
The Correct Answer and Explanation is:
Correct Answer:
- Original Slope: −1/2
- Parallel Slope: −1/2
Explanation:
To find the slope of the given line (the brown line), we identify two points it passes through: (−10, 5) and (10, −5). Using the slope formula m=y2−y1x2−x1m = \dfrac{y_2 – y_1}{x_2 – x_1}, we substitute the coordinates: m=−5−510−(−10)=−1020=−12m = \dfrac{-5 – 5}{10 – (-10)} = \dfrac{-10}{20} = -\dfrac{1}{2}.
This slope tells us the line falls one unit vertically for every two units it moves horizontally to the right. A parallel line must have the exact same slope, so the parallel line you graphed must also have a slope of −1/2.
In the image, you drew the green line passing through (−10, 0) and (10, −10). Let’s verify its slope:
m=−10−010−(−10)=−1020=−12m = \dfrac{-10 – 0}{10 – (-10)} = \dfrac{-10}{20} = -\dfrac{1}{2}
That confirms it. The green line is indeed parallel to the brown line because it has the same slope and does not intersect the original line. In geometry, lines that share the same slope but are not the same line will never meet. This property holds true for all parallel lines on a plane.
Understanding this concept visually strengthens your grasp on linear equations and graphing. It also reinforces how consistent slope governs the direction and spacing of lines. With graphing software offering instant feedback through color changes, you can better appreciate how algebraic concepts behave in two-dimensional space.
