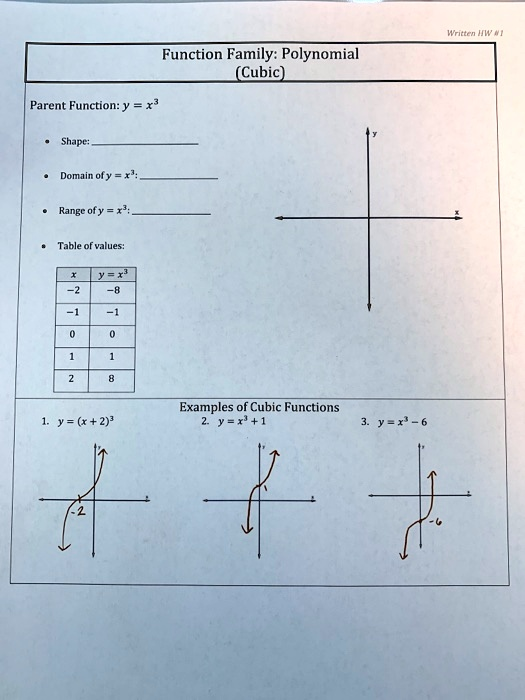
Function Family: Polynomial (Cubic) Parent Function: y = x^3 Shape: Domain: All real numbers Table of values: Examples of Cubic Functions Y = x^3 Y = (x + 2)^3 Range: All real numbers
The Correct Answer and Explanation is:
Cubic Function Overview
- Function Family: Polynomial
- Parent Function: y=x3y = x^3
- Shape: An S-shaped curve that passes through the origin, decreasing on the left and increasing on the right
- Domain: All real numbers (−∞, ∞)
- Range: All real numbers (−∞, ∞)
- Table of Values for y=x3y = x^3:
| xx | y=x3y = x^3 |
|---|---|
| −2 | −8 |
| −1 | −1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 8 |
- Examples of Cubic Functions:
- y=(x+2)3y = (x + 2)^3
- y=x3+1y = x^3 + 1
- y=x3−6y = x^3 – 6
Explanation A cubic function is a type of polynomial where the highest power of xx is 3. The parent function y=x3y = x^3 serves as the basic form from which all cubic transformations are derived. Its graph has a distinct S-shape and passes through the origin. For every real number xx, there exists a corresponding unique yy value, which confirms both its domain and range extend across all real numbers.
The function increases steadily for large positive and negative values, but in a non-linear way. Around the origin, the slope changes rapidly, which gives the graph its characteristic curvature. The function is odd and symmetric with respect to the origin, meaning rotating the graph 180 degrees about the origin gives the same graph.
Transformations of the parent function help to visualize how different terms affect its graph. For example, y=(x+2)3y = (x + 2)^3 is a horizontal shift to the left by two units. Similarly, adding or subtracting constants outside the cube function, as in y=x3+1y = x^3 + 1 or y=x3−6y = x^3 – 6, results in vertical shifts.
Understanding cubic functions is important because they appear in real-world contexts involving volume, economics, and physics, especially where growth or change occurs at a non-linear rate.
