Find the percent overshoot, settling time, rise time, and peak time for a.
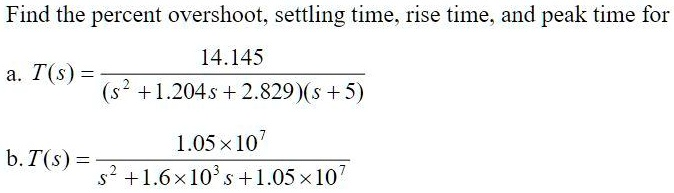
The Correct Answer and Explanation is:
Here is the solution for the given control systems problem.
This problem requires calculating key performance metrics for two systems based on their transfer functions. These metrics, including percent overshoot, settling time, rise time, and peak time, are standard measures for the transient response of a system, typically analyzed using a second-order system model.
a. For T(s) = 14.145 / ((s² + 1.204s + 2.829)(s + 5))
This is a third-order system. To find the performance metrics, we can use a second-order approximation because one pole is much farther from the imaginary axis than the other two dominant complex conjugate poles. The poles are at s = -5 and s ≈ -0.602 ± j1.57. Since the real pole at -5 is more than five times farther than the real part of the complex poles (-0.602), we can approximate the system by considering only the dominant poles from the quadratic term.
The approximating second-order transfer function is:
T_approx(s) = 2.829 / (s² + 1.204s + 2.829)
We match this to the standard form T(s) = ωn² / (s² + 2ζωn s + ωn²).
- Natural Frequency (ωn):
ωn² = 2.829 => ωn ≈ 1.682 rad/s - Damping Ratio (ζ):
2ζωn = 1.204 => ζ = 1.204 / (2 * 1.682) ≈ 0.358
Using these values, we calculate the performance metrics:
- Percent Overshoot (%OS): %OS = 100 * e^(-ζπ / √(1-ζ²)) ≈ 30.0%
- Settling Time (Ts, 2% criterion): Ts ≈ 4 / (ζωn) = 4 / (0.602) ≈ 6.64 s
- Peak Time (Tp): Tp = π / (ωn√(1-ζ²)) = π / 1.57 ≈ 2.00 s
- Rise Time (Tr, 10-90%): Tr ≈ (π – arccos(ζ)) / (ωn√(1-ζ²)) ≈ 1.24 s
b. For T(s) = (1.05 × 10⁷) / (s² + 1.6 × 10³ s + 1.05 × 10⁷)
This is a standard second-order system, so we can directly extract the parameters by comparing it to the standard form.
- Natural Frequency (ωn):
ωn² = 1.05 × 10⁷ => ωn ≈ 3240 rad/s - Damping Ratio (ζ):
2ζωn = 1.6 × 10³ => ζ = (1.6 × 10³) / (2 * 3240) ≈ 0.247
Now, we calculate the performance metrics:
- Percent Overshoot (%OS): %OS = 100 * e^(-ζπ / √(1-ζ²)) ≈ 44.9%
- Settling Time (Ts, 2% criterion): Ts ≈ 4 / (ζωn) = 4 / 800 = 0.005 s or 5.0 ms
- Peak Time (Tp): Tp = π / (ωn√(1-ζ²)) = π / 3140 ≈ 0.001 s or 1.0 ms
- Rise Time (Tr, 10-90%): Tr ≈ (π – arccos(ζ)) / (ωn√(1-ζ²)) ≈ 0.00058 s or 0.58 ms
thumb_upthumb_down
