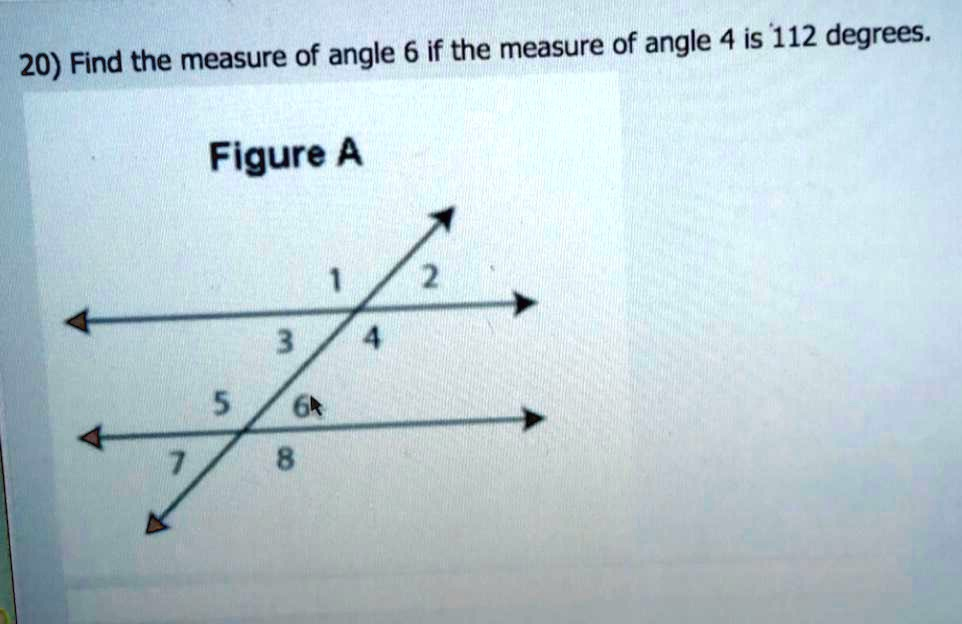
Find the measure of angle 6 if the measure of angle 4 is 112 degrees. Figure A 1 2 3 4 5 6 7 8
The Correct Answer and Explanation is:
The measure of angle 6 is 112 degrees.
Here’s a step-by-step explanation of how we arrive at that:
In the diagram, two parallel lines are intersected by a transversal, creating eight angles labeled 1 through 8. These angles form specific pairs with predictable relationships based on geometric rules.
We’re given that the measure of angle 4 is 112 degrees. To find angle 6, we trace its relationship to angle 4 using angle pair definitions:
- Angle 4 and angle 8 are corresponding angles. They are located on the same side of the transversal and in matching corners (angle 4 is above the top line on the right, and angle 8 is above the bottom line on the right). Since the lines are parallel, corresponding angles are congruent. This means angle 8 also measures 112 degrees.
- Angle 8 and angle 6 are alternate interior angles. They lie between the two parallel lines and on opposite sides of the transversal. Alternate interior angles are congruent as well, so angle 6 equals angle 8.
Thus, angle 6 equals angle 8 which equals angle 4. Therefore, angle 6 measures 112 degrees.
This solution demonstrates the power of geometric reasoning. By recognizing the relationships between angle pairs formed by parallel lines and a transversal, we can deduce unknown values without directly measuring. Corresponding angles maintain equality across lines because they “match” in position relative to the transversal. Alternate interior angles are congruent because the lines they are between do not diverge or bend, preserving symmetry.
This kind of geometric logic forms a backbone of spatial reasoning across disciplines. Whether it’s reading molecular structures, designing architectural plans, or coding computer graphics, recognizing symmetries and transformations is an essential skill.
