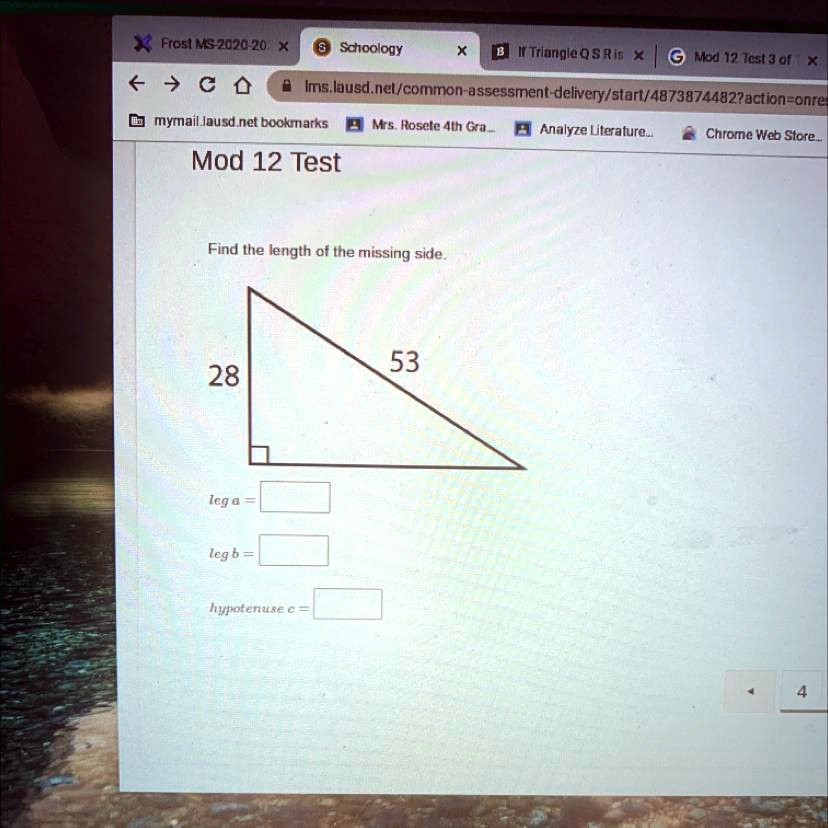
Find the length of the missing side. 53 28 leg a = leg b = hypotenuse c =
The Correct Answer and Explanation is:
To solve this right triangle problem, we’re given:
- One leg = 28 units
- Hypotenuse = 53 units
- We are missing the length of the other leg.
Step-by-step solution using the Pythagorean Theorem
The Pythagorean Theorem says:a2+b2=c2a^2 + b^2 = c^2a2+b2=c2
Where:
- aaa and bbb are the legs,
- ccc is the hypotenuse.
Here:
- One leg a=28a = 28a=28
- Hypotenuse c=53c = 53c=53
- We need to find the other leg bbb
282+b2=53228^2 + b^2 = 53^2282+b2=532784+b2=2809784 + b^2 = 2809784+b2=2809b2=2809−784=2025b^2 = 2809 – 784 = 2025b2=2809−784=2025b=2025=45b = \sqrt{2025} = 45b=2025=45
Final answers:
- leg a = 28
- leg b = 45
- hypotenuse c = 53
Explanation
This problem is a classic example of a right triangle where you’re given one leg and the hypotenuse and need to find the missing leg. In geometry, right triangles follow a special relationship called the Pythagorean Theorem. This theorem helps relate the lengths of the sides of a right triangle using squares of the lengths.
The theorem formula is:a2+b2=c2a^2 + b^2 = c^2a2+b2=c2
Here, ccc must always be the hypotenuse (the longest side, across from the right angle), while aaa and bbb are the two shorter legs.
In this question, the triangle has a right angle, with one leg given as 28 and the hypotenuse as 53. We’re missing the second leg. So, we plug the known values into the formula:
Square the known leg: 282=78428^2 = 784282=784
Square the hypotenuse: 532=280953^2 = 2809532=2809
Now subtract the square of the known leg from the square of the hypotenuse to isolate the unknown leg:b2=2809−784=2025b^2 = 2809 – 784 = 2025b2=2809−784=2025
Take the square root of 2025 to get the missing leg:2025=45\sqrt{2025} = 452025=45
So, the missing leg is 45. This process not only gives us the correct side length but also demonstrates how the Pythagorean Theorem applies to real problems.✅📐
