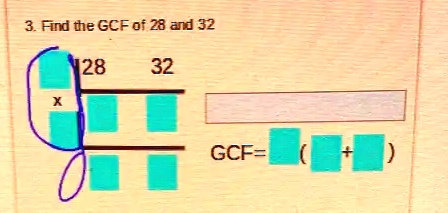
Find the GCF of 28 and 32 28 32 X GCF= ( +
The Correct Answer and Explanation is:
The correct answer is 4.
Explanation
The Greatest Common Factor, or GCF, is the largest positive integer that divides two or more numbers evenly, without leaving a remainder. To find the GCF of 28 and 32, we can use a couple of reliable methods.
Method 1: Listing the Factors
This straightforward method involves listing all the factors for each number and identifying the largest one they have in common.
- Factors of 28: 1, 2, 4, 7, 14, 28
- Factors of 32: 1, 2, 4, 8, 16, 32
By comparing these two lists, we can see that the numbers they share are 1, 2, and 4. The largest of these common factors is 4. Therefore, the GCF of 28 and 32 is 4.
Method 2: The Ladder or Prime Factorization Method
This method, which is hinted at in the image, involves continuously dividing the numbers by their common prime factors.
- Start by writing the two numbers, 28 and 32, next to each other.
- Find a prime number that divides both. Since both are even, we can divide by 2.
- 28 ÷ 2 = 14
- 32 ÷ 2 = 16
- Now, look at the new numbers, 14 and 16. They are also both even, so we can divide by 2 again.
- 14 ÷ 2 = 7
- 16 ÷ 2 = 8
- We are left with 7 and 8. These two numbers do not share any common factors other than 1, so we stop the process here.
- To find the GCF, multiply the prime factors we used to divide. In this case, we used 2 and 2.
GCF = 2 × 2 = 4
Both methods confirm that the GCF of 28 and 32 is 4. The format in the image shows how the GCF can be used with the distributive property, where you can express the sum of the numbers as GCF × (quotient1 + quotient2), or 4 × (7 + 8).
