The Correct Answer and Explanation is:
The correct answer is:
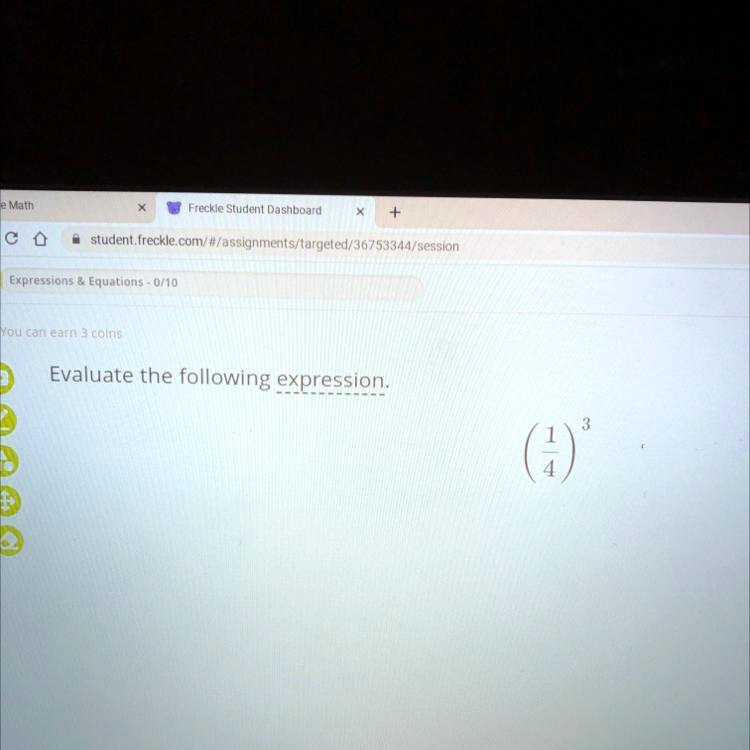
(14)3=164\left( \frac{1}{4} \right)^3 = \frac{1}{64}
To evaluate the expression (14)3(\frac{1}{4})^3, we are asked to raise the fraction 14\frac{1}{4} to the third power. This means we multiply 14\frac{1}{4} by itself three times. In mathematical terms:
(14)3=14×14×14\left( \frac{1}{4} \right)^3 = \frac{1}{4} \times \frac{1}{4} \times \frac{1}{4}
The multiplication of fractions follows a straightforward rule. Multiply the numerators together and then multiply the denominators. In this case, all the numerators are 1, and all the denominators are 4:
1×1×14×4×4=164\frac{1 \times 1 \times 1}{4 \times 4 \times 4} = \frac{1}{64}
This result tells us that (14)3\left(\frac{1}{4}\right)^3 is equal to 164\frac{1}{64}.
This problem offers a great opportunity to reinforce the concept of exponentiation with fractions. Exponentiation is the repeated multiplication of a number by itself. When the base is a fraction, both the numerator and denominator are raised to the given power. Since our base is 14\frac{1}{4}, we cube the numerator and the denominator individually.
1343=164\frac{1^3}{4^3} = \frac{1}{64}
This principle applies generally. For any fraction ab\frac{a}{b}, raising it to the power nn results in anbn\frac{a^n}{b^n}.
Understanding this foundational concept is essential for more advanced mathematics. It supports work in algebra, scientific notation, and problem-solving involving scale and ratios. By mastering simple exponentiation with fractions like this, learners build confidence and accuracy that will serve them in more complex expressions.
