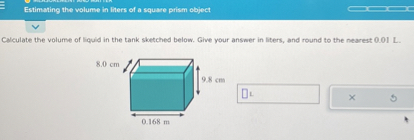
Estimating the volume in liters of a square prism object Calculate the volume of liquid in the tank sketched below. Give your answer in liters, and round to the nearest
.
The Correct Answer and Explanation is:
To find the volume of liquid in the tank, we use the formula for the volume of a rectangular (square-based) prism:
Volume=length×width×height\text{Volume} = \text{length} \times \text{width} \times \text{height}
From the image, the dimensions of the tank are:
- Length = 0.168 meters = 16.8 centimeters
- Width = 9.8 centimeters
- Height = 8.0 centimeters
Since 1 liter is equal to 1000 cubic centimeters, we will calculate the volume in cubic centimeters first, then convert to liters.
Volume=16.8×9.8×8.0=1315.2 cm3\text{Volume} = 16.8 \times 9.8 \times 8.0 = 1315.2 \text{ cm}^3
Volume in liters=1315.21000=1.3152 L\text{Volume in liters} = \frac{1315.2}{1000} = 1.3152 \text{ L}
Rounded to the nearest hundredth:
1.32 liters\boxed{1.32 \text{ liters}}
Explanation
To estimate the volume of a liquid contained within a square or rectangular prism-shaped tank, it is essential to multiply the tank’s internal dimensions: the length, width, and height. These dimensions must all be in the same unit to ensure accuracy. In this case, while two dimensions were given in centimeters, the length was provided in meters. To align units, the length must be converted to centimeters by multiplying by 100. Thus, 0.168 meters becomes 16.8 centimeters.
With all dimensions now in centimeters, the volume can be determined using the standard geometric formula for the volume of a prism. This gives us a volume in cubic centimeters, a measure of how much three-dimensional space the liquid occupies. However, because the problem asks for the result in liters, a unit conversion must follow. Since 1 liter is equivalent to 1000 cubic centimeters, dividing the result by 1000 yields the volume in liters.
The final step is rounding. Since measurements in practical contexts like fluid storage often require clarity and ease of interpretation, the result is rounded to the nearest hundredth of a liter. This gives an accurate, user-friendly answer: 1.32 liters.
This process reinforces the importance of unit consistency and conversion in applied science. It also illustrates how foundational geometry links directly to real-world measurements in fields like chemistry, biology, and engineering, where volumes of liquids must be precisely calculated. The clarity and structure of the solution ensure both mathematical soundness and practical relevance.
