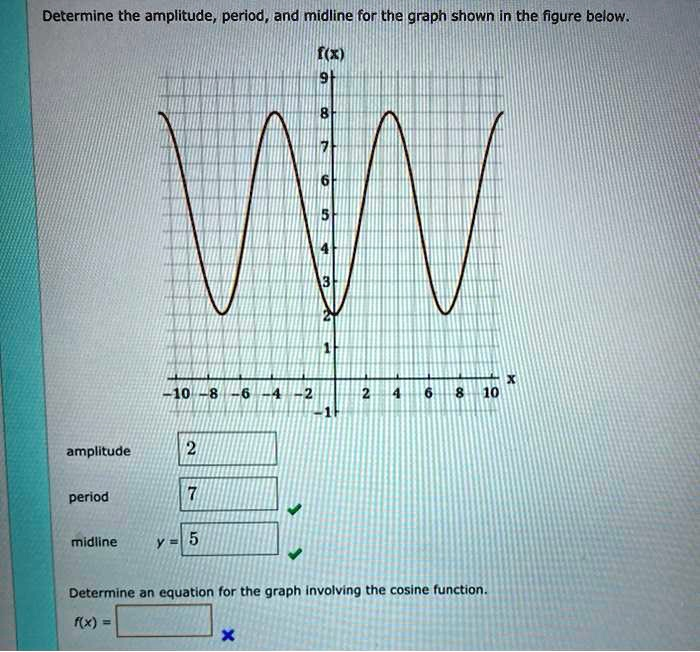
Determine the amplitude, period, and midline for the graph shown in the figure below. f(x) 9 8 7 6 5 4 3 2 1 -10 -8 -6 -4 -2 2 4 6 8 10 -1 amplitude 2 period 7 midline y = 5 Determine an equation for the graph involving the cosine function. f(x) =
The Correct Answer and Explanation is:
Here are the correct values and the equation for the given graph, along with a step-by-step explanation.
1. Midline
The midline is the horizontal line that runs exactly halfway between the maximum and minimum values of the graph.
- From the graph, the maximum value (the highest point) is y = 8.
- The minimum value (the lowest point) is y = 2.
To find the midline, we calculate the average of the maximum and minimum values:
Midline = (Maximum Value + Minimum Value) / 2
Midline = (8 + 2) / 2 = 10 / 2 = 5
So, the midline is the line y = 5.
2. Amplitude
The amplitude is the distance from the midline to either a maximum or minimum point. It is half of the total height of the wave.
Amplitude = (Maximum Value – Minimum Value) / 2
Amplitude = (8 – 2) / 2 = 6 / 2 = 3
Thus, the amplitude is 3.
(Note: The value of 2 entered in the image for the amplitude is incorrect).
3. Period
The period is the horizontal length of one complete cycle. We can find this by measuring the horizontal distance between two consecutive minimums or maximums.
- The graph has a minimum at x = 0.
- The next minimum occurs at x = 7.
Period = (x-coordinate of second minimum) – (x-coordinate of first minimum)
Period = 7 – 0 = 7
Therefore, the period is 7.
4. Equation of the Function
We need to find an equation in the form f(x) = Acos(B(x – C)) + D.
- A is the amplitude. We found the amplitude is 3. However, the graph has a minimum at x=0, while a standard cosine function starts at a maximum. This indicates a vertical reflection, so we use A = -3.
- D is the midline. We found the midline is y = 5, so D = 5.
- B relates to the period. The formula is Period = 2π/B. We know the period is 7, so 7 = 2π/B. Solving for B gives B = 2π/7.
- C is the phase shift. Since we used a reflected cosine (A = -3) which starts at a minimum, and our graph also starts at a minimum at x=0, there is no horizontal shift. So, C = 0.
Plugging these values into the general equation:
f(x) = -3cos((2π/7)(x – 0)) + 5
This simplifies to the final equation:
f(x) = -3cos((2π/7)x) + 5
