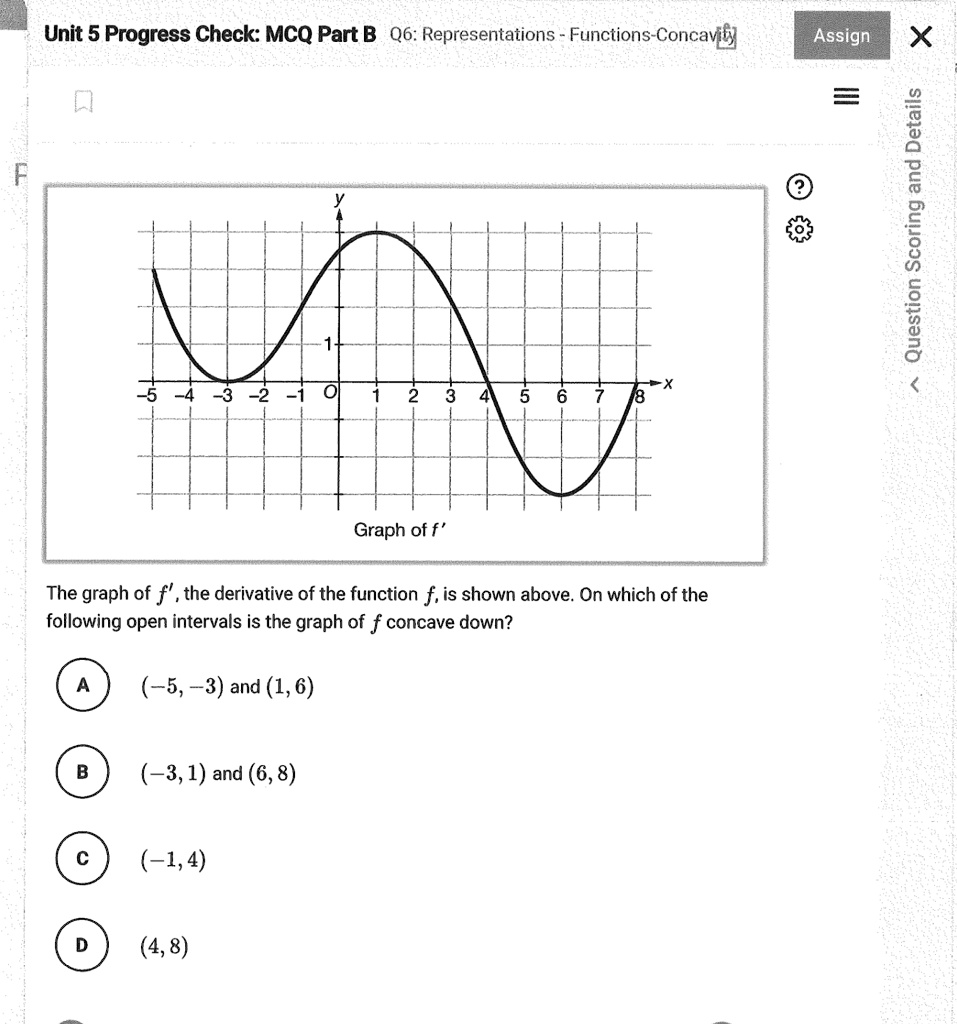
Concavity Assign 38 I J 70 23 Graph of f’ The graph of f’, the derivative of the function f, is shown above. On which of the following open intervals is the graph of f concave down? (-5, -3) and (1, 6) (-3, 1) and (6, 8) (-1, 4) (4, 8)
Unit 5 Progress Check: MCQ Part B Q6: Representations of Functions – Concavity Assign 38 I J 70 23 Graph of f’ The graph of f’, the derivative of the function f, is shown above. On which of the following open intervals is the graph of f concave down? (-5, -3) and (1, 6) (-3, 1) and (6, 8) (-1, 4) (4, 8)
The Correct Answer and Explanation is:
The correct answer is: (–5, –3) and (1, 6).
To determine where the function f is concave down, we analyze its second derivative f″(x). Since we’re given the graph of f′(x) (the first derivative), we must identify where f′(x) is decreasing. When f′(x) is decreasing, its slope is negative, which implies that f″(x) < 0, and thus f is concave down.
From the graph:
- On the interval (–5, –3), the graph of f′(x) clearly decreases from a higher positive value to a lower one. This indicates that the slope of f is decreasing, so f″(x) is negative. Therefore, f is concave down on this interval.
- On the interval (1, 6), the graph again shows a decreasing trend — f′(x) declines from a positive value, approaches zero, and may even become negative. This confirms that f″(x) remains negative over this interval, so f is concave down here as well.
Now consider the other choices:
- (–3, 1) contains a portion where f′(x) is increasing, meaning f″(x) is positive for at least part of it. So, f is not concave down throughout.
- (6, 8) shows a decreasing portion of f′(x), so f may be concave down there, but the interval alone is not paired with another correct one like in option A.
- (–1, 4) includes part of an increasing slope, which means f″(x) is positive there.
- (4, 8) also contains parts where the slope of f′(x) increases and then decreases, so the concavity isn’t consistently downward.
Thus, only the intervals (–5, –3) and (1, 6) reflect portions where f′(x) is strictly decreasing throughout, confirming the graph of f is concave down there.
