AB \parallel CD ; \theta = ?
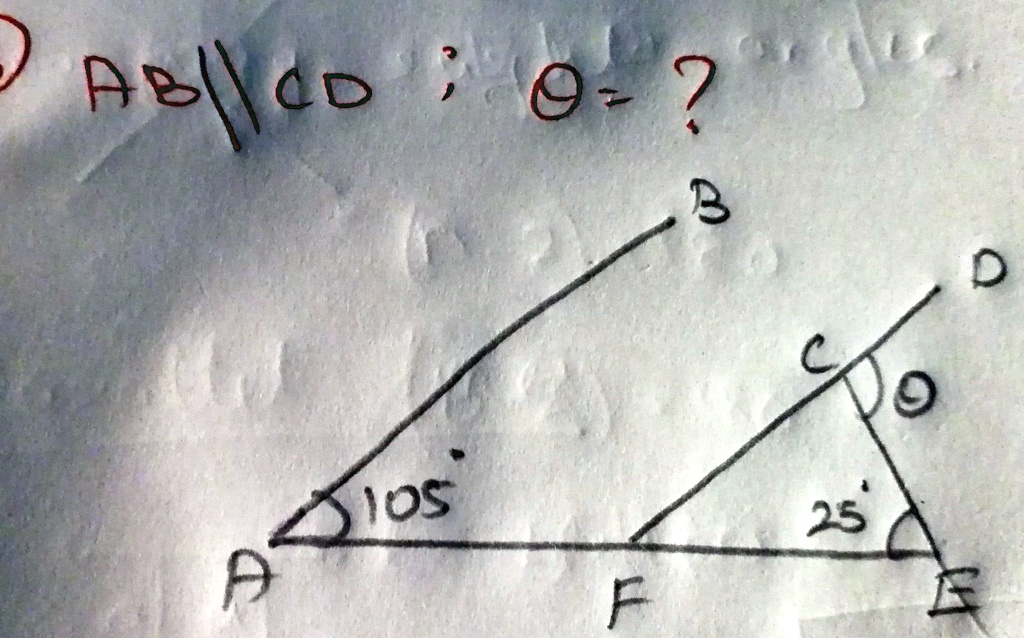
The Correct Answer and Explanation is:
The given diagram features two parallel lines AB and CD, with angles marked at different points. The angle θ at point C needs to be determined.
Since AB is parallel to CD, the angle at point A, which is 105 degrees, and the angle at point C are corresponding angles. Corresponding angles are equal when two lines are parallel. This means that the value of θ is 105 degrees.
To further verify this, we can analyze the alternate interior angles formed by the transversal that intersects the parallel lines AB and CD. The angle at point E, which is 25 degrees, and the angle at point C are alternate interior angles. Since AB is parallel to CD, alternate interior angles are also equal.
Through both the corresponding angles and alternate interior angles properties, we confirm that θ is indeed 105 degrees.
This problem illustrates fundamental principles in geometry. Parallel lines play a crucial role in determining angle relationships when intersected by a transversal. Understanding corresponding angles is essential. These angles appear in matching positions on either side of the transversal and retain equality when parallel lines are involved.
Similarly, alternate interior angles are positioned on opposite sides of the transversal but inside the two parallel lines. Their equality is a key property that simplifies angle calculations.
By recognizing these angle properties and their applications, we can systematically determine unknown values in geometric diagrams. This problem serves as a strong example of how parallel lines and transversals create predictable angle relationships, which are useful in various mathematical and engineering applications.
Thus, the angle θ at point C is 105 degrees, confirmed through both the corresponding and alternate interior angles approach.
