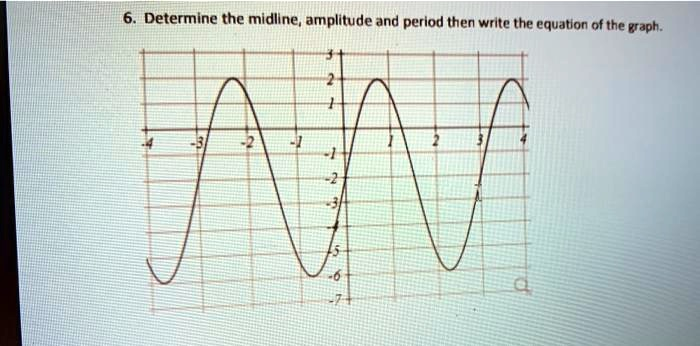
Determine the midline; amplitude and period then write the equation of the graph:
The Correct Answer and Explanation is:
=
Based on the provided graph, here are the determined characteristics and the corresponding equation.
Midline: The midline is the horizontal line that passes exactly halfway between the graph’s maximum and minimum points. First, we identify the maximum y-value, which is y = 2 (seen at x = -2 and x = 1). Next, we identify the minimum y-value, which is y = -6 (seen at x = -0.5 and x = 2.5). The midline is the average of these two values.
Midline = (Maximum Value + Minimum Value) / 2
Midline = (2 + (-6)) / 2 = -4 / 2 = -2
Therefore, the midline is the line y = -2.
Amplitude: The amplitude is the vertical distance from the midline to either a maximum or minimum point. It represents the height of the waves. It can be calculated as half the difference between the maximum and minimum values.
Amplitude = (Maximum Value – Minimum Value) / 2
Amplitude = (2 – (-6)) / 2 = 8 / 2 = 4
Thus, the amplitude is 4.
Period: The period is the horizontal length of one complete cycle of the wave. We can measure this distance from one peak to the next consecutive peak. The first visible peak is at x = -2, and the next peak is at x = 1.
Period = x₂ – x₁ = 1 – (-2) = 3
So, the period of the function is 3.
Equation of the Graph:
We can model the graph using a sine or cosine function in the form y = A cos(B(x – C)) + D or y = A sin(B(x – C)) + D.
- A is the amplitude, which is 4.
- D is the vertical shift, which is the midline, y = -2.
- B is related to the period (P) by the formula P = 2π / B. We found P = 3, so 3 = 2π / B, which gives B = 2π / 3.
- C is the phase shift, or horizontal shift. Let’s use a cosine function. A standard cosine function starts at its maximum value. This graph has a maximum at x = -2. This means the graph is shifted 2 units to the left, so C = -2.
Putting it all together into the cosine form:
y = A cos(B(x – C)) + D
y = 4 cos( (2π/3)(x – (-2)) ) – 2
The final equation is:
y = 4 cos( (2π/3)(x + 2) ) – 2
