For the process CHCl2(s) → CHCl3(l), ΔH = 9.17 kJ/mol and ΔS = 43.9 J/molK. What is the melting point of chloroform? 64 °C (62209 %€ 1.17 K; Joule: Ag A4 T4$ 130 % 9.17 × 10^3 (43.9 × 64) % -130 % K+2s: 9.17 × 10^3 T( = 3.08 × 10^-3 43.9 s/mole
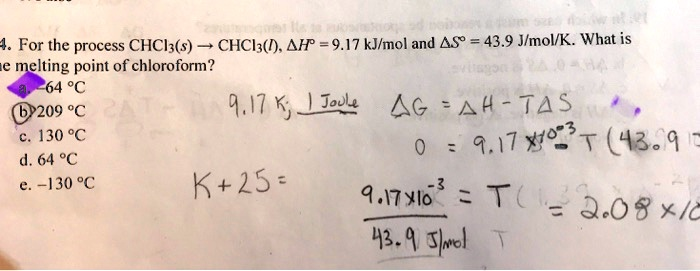
The Correct Answer and Explanation is:
Correct Answer: a. -64 °C
Explanation:
To find the melting point of chloroform, we need to determine the temperature at which the solid and liquid phases are in equilibrium. The provided chemical equation, CHCl₃(s) → CHCl₃(l), describes this melting process. According to the principles of thermodynamics, a system at equilibrium, such as a substance at its melting or boiling point, has a Gibbs free energy change (ΔG) equal to zero.
The Gibbs free energy equation relates enthalpy (ΔH), entropy (ΔS), and temperature (T):
ΔG = ΔH – TΔS
For a phase change at equilibrium, we can set ΔG to 0.
0 = ΔH – TΔS
This equation can be rearranged to solve for the temperature (T), which in this case represents the melting point.
TΔS = ΔH
T = ΔH / ΔS
Before calculating, it is crucial to ensure that the units are consistent. The problem provides ΔH° in kilojoules (kJ/mol) and ΔS° in joules per mole Kelvin (J/mol·K). We must convert one of the units to match the other. Let’s convert ΔH° from kilojoules to joules.
ΔH° = 9.17 kJ/mol × (1000 J / 1 kJ) = 9170 J/mol
Now, we can substitute the values for ΔH° and ΔS° into the formula to find the temperature in Kelvin (K).
T = (9170 J/mol) / (43.9 J/mol·K)
T ≈ 208.9 K
The multiple choice options are in degrees Celsius (°C), so a final conversion from Kelvin to Celsius is necessary.
T(°C) = T(K) – 273.15
T(°C) = 208.9 K – 273.15
T(°C) ≈ -64.25 °C
The calculated melting point is approximately -64.25 °C. This value is closest to option (a), making -64 °C the correct answer.
