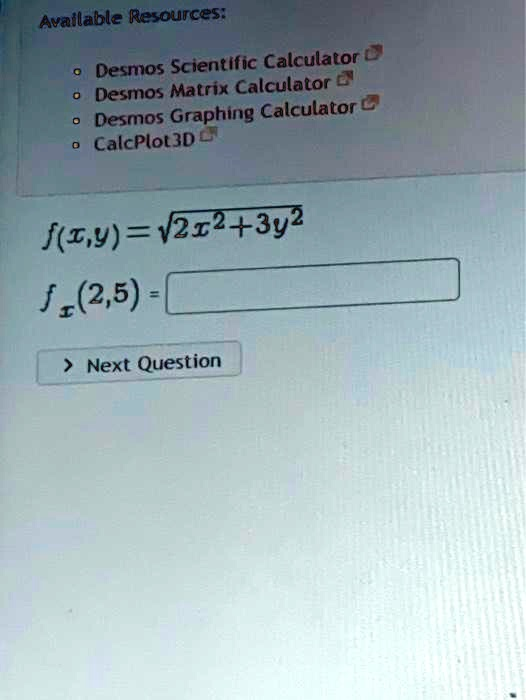
Available Resources: • Desmos Scientific Calculator • Desmos Matrix Calculator • Desmos Graphing Calculator • CalcPlot3D f(x,y)=\sqrt{2x^2+3y^2} f(2,5) =
The Correct Answer and Explanation is:
Answer:
The correct answer is 4/√83.
Explanation:
The problem asks for the value of the partial derivative of the function f(x,y) = √(2x² + 3y²) with respect to x, evaluated at the point (2, 5). This is denoted by f_x(2,5). The process involves two main steps: first finding the partial derivative function f_x(x,y) and then substituting the given values for x and y.
Step 1: Find the partial derivative f_x(x,y)
To find the partial derivative with respect to x, we treat the variable y as a constant. The function can be rewritten using a fractional exponent, which makes applying differentiation rules easier:
f(x,y) = (2x² + 3y²)^(1/2)
We will use the chain rule for differentiation. Let the inner function be u = 2x² + 3y². The outer function is u^(1/2).
- Differentiate the outer function with respect to u:
d/du (u^(1/2)) = (1/2)u^(-1/2) - Differentiate the inner function u with respect to x, treating y² as a constant:
∂u/∂x = ∂/∂x (2x² + 3y²) = 4x + 0 = 4x - Apply the chain rule by multiplying the results from the first two parts:
f_x(x,y) = (1/2)(2x² + 3y²)^(-1/2) * (4x)
Simplifying this expression gives us:
f_x(x,y) = (4x) / (2√(2x² + 3y²)) = 2x / √(2x² + 3y²)
Step 2: Evaluate f_x(2,5)
Now, we substitute x = 2 and y = 5 into the expression for f_x(x,y):
f_x(2,5) = (2 * 2) / √(2 * (2)² + 3 * (5)²)
Calculate the numerator:
2 * 2 = 4
Calculate the expression inside the square root in the denominator:
2 * (2)² + 3 * (5)² = 2 * 4 + 3 * 25 = 8 + 75 = 83
So the expression becomes:
f_x(2,5) = 4 / √83
The final value of the partial derivative at the point (2, 5) is 4/√83.thumb_upthumb_down
