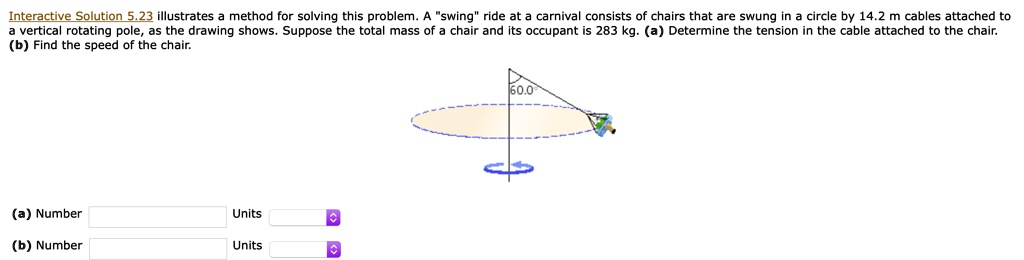
Interactive Solution 5.23 illustrates method for solving this problem: swing’ ride at carnival consists of chairs that are swung in circle by 14.2 m cables attached to vertica rotating pole as the drawing shows_ Suppose the total mass f chair and its occupant is 283 kg; (a) Determine the tension in the cable attached to the chair (b) Find the speed of the chair: 60,0 (a) Number Units (b) Number Units
The Correct Answer and Explanation is:
To solve this problem, we analyze the forces acting on the chair in circular motion. The chair is suspended by a cable of length 14.2 m and swings at an angle of 60.0° from the vertical. The total mass of the chair and occupant is 283 kg.
(a) Tension in the Cable
We resolve the tension TT into two components:
- Vertical component: Tcos(θ)=mgT \cos(\theta) = mg
- Horizontal component: Tsin(θ)=mv2rT \sin(\theta) = \frac{mv^2}{r}
From the vertical component:
T=mgcos(θ)T = \frac{mg}{\cos(\theta)}
Substitute values:
T=(283 kg)(9.81 m/s2)cos(60.0∘)=2776.230.5=5552.46 NT = \frac{(283 \, \text{kg})(9.81 \, \text{m/s}^2)}{\cos(60.0^\circ)} = \frac{2776.23}{0.5} = 5552.46 \, \text{N}
Answer (a): Tension T=5552 NT = 5552 \, \text{N}
(b) Speed of the Chair
First, find the radius rr of the circular path:
r=Lsin(θ)=14.2 m⋅sin(60.0∘)=14.2⋅0.866=12.3 mr = L \sin(\theta) = 14.2 \, \text{m} \cdot \sin(60.0^\circ) = 14.2 \cdot 0.866 = 12.3 \, \text{m}
Now use the horizontal component:
Tsin(θ)=mv2rT \sin(\theta) = \frac{mv^2}{r}
v2=Tsin(θ)⋅rmv^2 = \frac{T \sin(\theta) \cdot r}{m}
v2=5552.46⋅0.866⋅12.3283=5924.5283=20.94v^2 = \frac{5552.46 \cdot 0.866 \cdot 12.3}{283} = \frac{5924.5}{283} = 20.94
v=20.94=4.58 m/sv = \sqrt{20.94} = 4.58 \, \text{m/s}
Answer (b): Speed v=4.58 m/sv = 4.58 \, \text{m/s}
Explanation
This problem involves circular motion where the tension in the cable provides both the centripetal force and supports the weight of the chair and rider. By resolving the tension into vertical and horizontal components, we can isolate the gravitational force and the centripetal force. The vertical component balances the weight, while the horizontal component provides the necessary centripetal force to keep the chair moving in a circle. Using trigonometric relationships and Newton’s second law, we calculate the tension and then use it to find the speed of the chair.
