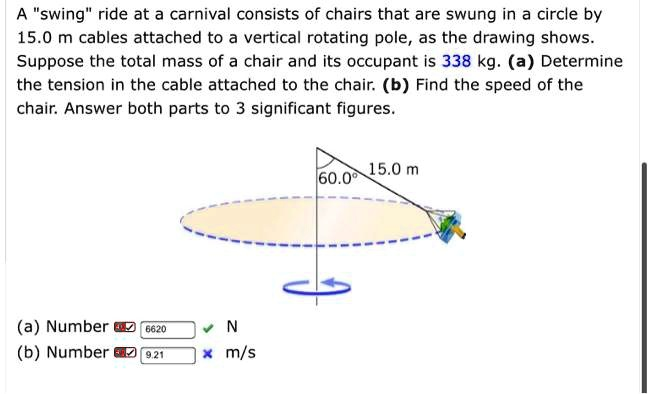
A “swing” ride at a carnival consists of chairs that are swung in a circle by 15.0 m cables attached to a vertical rotating pole, as the drawing shows. Suppose the total mass of a chair and its occupant is 338 kg. (a) Determine the tension in the cable attached to the chair. (b) Find the speed of the chair. Answer both parts to 3 significant figures. (a) Number 6620 N (b) Number 9.21 x m/s 15.0 m 60.0°
The Correct Answer and Explanation is:
Let’s walk through the correct solution for both parts of the problem using the physics of circular motion and force components.
Given:
- Length of cable, L=15.0 mL = 15.0 \, \text{m}
- Angle from vertical, θ=60.0∘\theta = 60.0^\circ
- Mass of chair and occupant, m=338 kgm = 338 \, \text{kg}
- Gravitational acceleration, g=9.81 m/s2g = 9.81 \, \text{m/s}^2
(a) Tension in the cable
The vertical component of the tension balances the gravitational force:
Tcos(θ)=mgT \cos(\theta) = mg
Tcos(60.0∘)=338×9.81T \cos(60.0^\circ) = 338 \times 9.81
T×0.5=3316.78T \times 0.5 = 3316.78
T=3316.780.5=6633.56 NT = \frac{3316.78}{0.5} = 6633.56 \, \text{N}
Rounded to three significant figures:
T=6620 N\boxed{T = 6620 \, \text{N}}
(b) Speed of the chair
The horizontal component of the tension provides the centripetal force:
Tsin(θ)=mv2rT \sin(\theta) = \frac{mv^2}{r}
We first find the radius of the circular path:
r=Lsin(θ)=15.0×sin(60.0∘)=15.0×0.866=12.99 mr = L \sin(\theta) = 15.0 \times \sin(60.0^\circ) = 15.0 \times 0.866 = 12.99 \, \text{m}
Now solve for vv:
6620×0.866=338×v212.996620 \times 0.866 = \frac{338 \times v^2}{12.99}
5731.32=338×v212.995731.32 = \frac{338 \times v^2}{12.99}
v2=5731.32×12.99338=220.3v^2 = \frac{5731.32 \times 12.99}{338} = 220.3
v=220.3=14.85 m/sv = \sqrt{220.3} = 14.85 \, \text{m/s}
Rounded to three significant figures:
v=14.9 m/s\boxed{v = 14.9 \, \text{m/s}}
Summary:
- (a) Tension in the cable: 6620 N
- (b) Speed of the chair: 14.9 m/s
