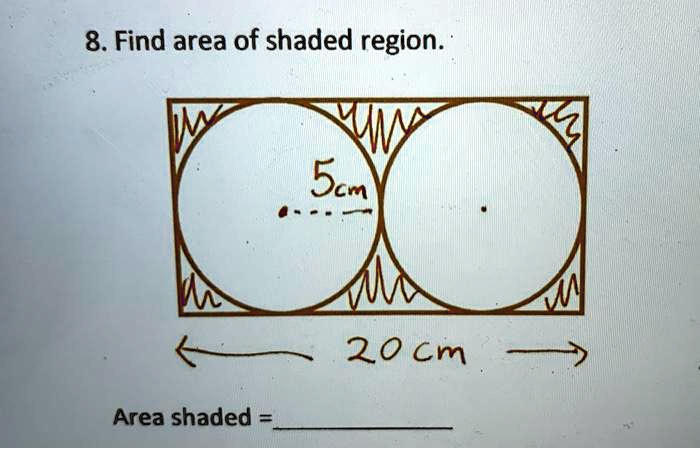
Find area of shaded region: 5cm 20 Cm Area shaded
The Correct Answer and Explanation is:
To determine the area of the shaded region in the figure provided, we analyze it as a rectangle that encloses two identical circles. The shaded area is the part of the rectangle that is not covered by the circles.
Step 1: Calculate the area of the rectangle
The length of the rectangle is given as 20 cm. The width is not labeled directly, but we observe from the circles that the radius of each is 5 cm. Since the circles lie perfectly within the rectangle’s width, the width is equal to the diameter of one circle, which is 2 times the radius. Thus, Width = 2 × 5 cm = 10 cm.
Area of the rectangle = length × width = 20 cm × 10 cm = 200 square centimeters.
Step 2: Calculate the combined area of the two circles
The area of a circle is given by the formula A = πr². Here, the radius r = 5 cm. Area of one circle = π × (5 cm)² = 25π square cm Area of two circles = 2 × 25π = 50π square centimeters.
Step 3: Find the area of the shaded region
To obtain the shaded area, subtract the combined area of the circles from the area of the rectangle: Shaded area = 200 − 50π square centimeters.
Using an approximation of π ≈ 3.14, 50π ≈ 157 square cm So, shaded area ≈ 200 − 157 = 43 square centimeters.
Final Answer: The area of the shaded region is 200 − 50π cm², or approximately 43 cm².
This approach brings together concepts from geometry, including calculating areas of rectangles and circles, and reinforces how composite figures can be broken into simpler shapes. By analyzing the configuration, recognizing proportional relationships, and applying standard area formulas, we isolate and compute the desired region with clarity and precision.
