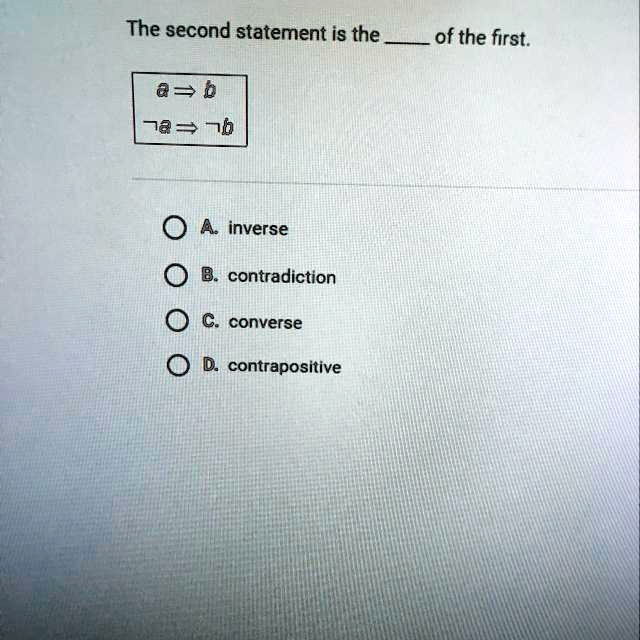
The second statement is the ____ of the first.
The Correct Answer and Explanation is:
Correct answer: D. Contrapositive
To analyze the relationship between the two statements “a implies b” and “not b implies not a,” we apply the concept of logical equivalence in propositional logic. The original statement, “a implies b” (symbolically represented as a → b), means that if a is true, then b must also be true. The second statement, “not b implies not a” (¬b → ¬a), rearranges and negates both components of the original statement. This transformation is precisely what defines the contrapositive of a conditional statement.
Understanding the contrapositive begins with the structure of a conditional. For any implication p → q, its contrapositive is ¬q → ¬p. This transformation not only changes the direction of implication but also applies logical negation to both the hypothesis and the conclusion. Crucially, the contrapositive is always logically equivalent to the original implication. That is, if the original statement is true, the contrapositive must also be true under all truth conditions.
By contrast, the converse of a → b would be b → a, which simply switches the positions of a and b without applying negation. The inverse, ¬a → ¬b, negates both statements without reversing them. Neither the converse nor the inverse is logically equivalent to the original statement in all cases.
A contradiction, on the other hand, refers to a compound statement that is always false regardless of the truth values of its components. The second statement here is not inherently false and therefore cannot be a contradiction.
Thus, not b implies not a is the contrapositive of a implies b. This equivalence is a cornerstone of formal proofs and logical reasoning, as proving the contrapositive of a statement is often more straightforward than proving the original form
