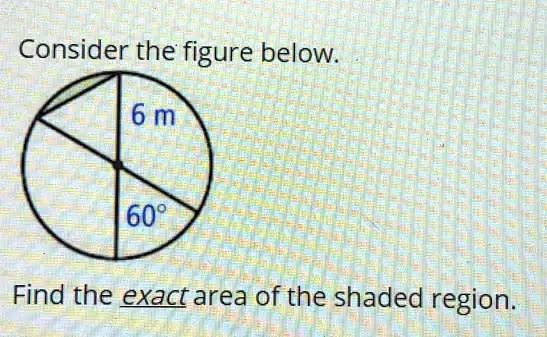
Consider the figure below. 6 m 60° Find the exact area of the shaded region.
The Correct Answer and Explanation is:
To find the exact area of the shaded region in a circle with radius 6 meters and central angle 60°, we use the formula for the area of a sector:
Area of sector=θ360×πr2\text{Area of sector} = \frac{\theta}{360} \times \pi r^2
Given:
- θ=60∘\theta = 60^\circ
- r=6 mr = 6 \, \text{m}
Substituting into the formula:
Area=60360×π×(6)2=16×π×36=6π m2\text{Area} = \frac{60}{360} \times \pi \times (6)^2 = \frac{1}{6} \times \pi \times 36 = 6\pi \, \text{m}^2
Exact area of the shaded region: 6π m26\pi \, \text{m}^2
To understand this result, consider the structure of a circle. A full circle has 360 degrees. If you take a piece of that circle defined by a central angle (like slicing a pizza), you create what is called a sector. The area of this sector depends on the angle of the slice in proportion to the whole circle, as well as the square of the radius.
Here, the central angle is 60 degrees. That means the shaded portion represents one sixth of the entire circle. To find the total area of the circle, we apply the formula πr2\pi r^2. With a radius of 6 meters, the total area becomes 36π m236\pi \, \text{m}^2. Since 60 degrees is one sixth of 360 degrees, we take one sixth of the full area.
Thus, the area of the shaded region is 16×36π=6π m2\frac{1}{6} \times 36\pi = 6\pi \, \text{m}^2. This result is left in terms of π\pi because the problem asked for an exact value. Using decimals would introduce approximation.
This type of calculation is commonly used in both geometry and real-life applications involving circular segments, such as designing circular gardens, fan blades, or measuring portions of pie charts.
