ft ladder leaning against a wall forms an angle of θ with the ground
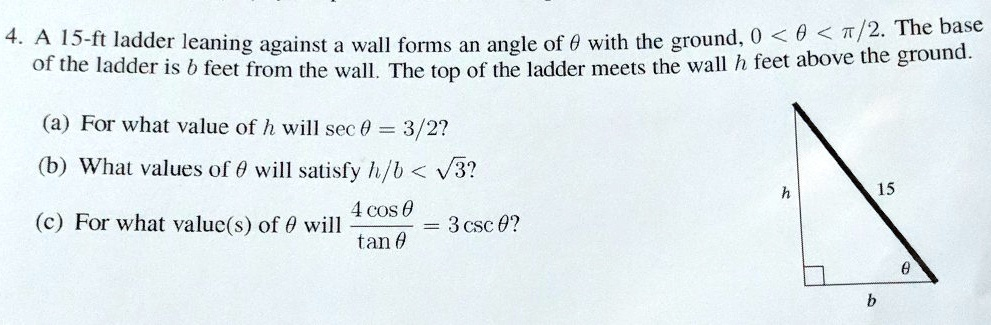
The Correct Answer and Explanation is:
Let’s walk through each part of the trigonometric ladder problem in a structured way:
Part (a): Given:
- A ladder of length 15 ft
- sec(θ) = 3/2
We know that sec(θ) is the reciprocal of cos(θ), so: cos(θ) = 2/3
From a right triangle formed by the wall, ground, and ladder, cos(θ) = adjacent / hypotenuse = b / 15 So, b = 15 × cos(θ) = 15 × (2/3) = 10 ft
Using the Pythagorean theorem: h² + b² = 15² h² + 100 = 225 h² = 125 h = √125 = 5√5 ft
Part (b): We want to find values of θ such that h / b < √3. From trigonometric relationships: h = 15 sin(θ) b = 15 cos(θ) Then, h / b = (15 sin(θ)) / (15 cos(θ)) = tan(θ) So, tan(θ) < √3
Taking the arctangent of both sides: θ < arctan(√3) = π/3
Therefore, all values of θ in the interval (0, π/3) will satisfy the condition.
Part (c): We solve: 4 cos(θ) / tan(θ) = 3 csc(θ)
Left side becomes: 4 cos(θ) / (sin(θ) / cos(θ)) = 4 cos²(θ) / sin(θ)
Right side is: 3 / sin(θ)
Equating both: 4 cos²(θ) / sin(θ) = 3 / sin(θ) => 4 cos²(θ) = 3 => cos²(θ) = 3/4 => cos(θ) = ±√3 / 2
This gives: θ = π/6 or θ = 5π/6 (within [0, π])
Only θ = π/6 is valid since 0 < θ < π/2 for a ladder angle.
So the final answers are:
- (a) h = 5√5 ft
- (b) θ < π/3
- (c) θ = π/6
