Solve the equation.\ \frac{3n}{n+2} – \frac{5}{n-4} = \frac{2n^2 – 14n}{n^2 – 2n – 8
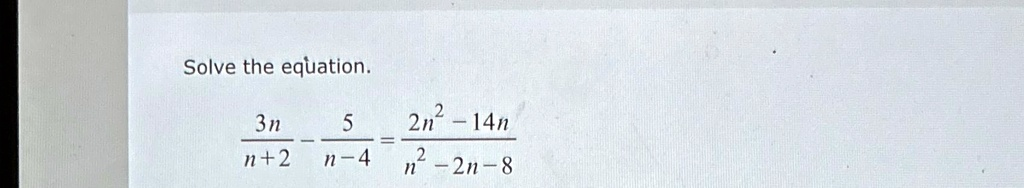
The Correct Answer and Explanation is:
We are given the equation:3nn+2−5n−4=2n2−14nn2−2n−8\frac{3n}{n+2} – \frac{5}{n-4} = \frac{2n^2 – 14n}{n^2 – 2n – 8}n+23n−n−45=n2−2n−82n2−14n
Step 1: Factor the denominator on the right-hand side
n2−2n−8=(n−4)(n+2)n^2 – 2n – 8 = (n – 4)(n + 2)n2−2n−8=(n−4)(n+2)
So the equation becomes:3nn+2−5n−4=2n2−14n(n−4)(n+2)\frac{3n}{n+2} – \frac{5}{n-4} = \frac{2n^2 – 14n}{(n-4)(n+2)}n+23n−n−45=(n−4)(n+2)2n2−14n
Step 2: Find the least common denominator (LCD)
The LCD is (n+2)(n−4)(n + 2)(n – 4)(n+2)(n−4). We will write all terms with this denominator.
Left-hand side:3nn+2=3n(n−4)(n+2)(n−4),5n−4=5(n+2)(n−4)(n+2)\frac{3n}{n+2} = \frac{3n(n – 4)}{(n + 2)(n – 4)}, \quad \frac{5}{n – 4} = \frac{5(n + 2)}{(n – 4)(n + 2)}n+23n=(n+2)(n−4)3n(n−4),n−45=(n−4)(n+2)5(n+2)
Now substitute:3n(n−4)−5(n+2)(n+2)(n−4)=2n2−14n(n+2)(n−4)\frac{3n(n – 4) – 5(n + 2)}{(n + 2)(n – 4)} = \frac{2n^2 – 14n}{(n + 2)(n – 4)}(n+2)(n−4)3n(n−4)−5(n+2)=(n+2)(n−4)2n2−14n
Step 3: Simplify the numerator on the left-hand side
3n(n−4)=3n2−12n,5(n+2)=5n+103n(n – 4) = 3n^2 – 12n, \quad 5(n + 2) = 5n + 103n(n−4)=3n2−12n,5(n+2)=5n+103n2−12n−5n−10=3n2−17n−103n^2 – 12n – 5n – 10 = 3n^2 – 17n – 103n2−12n−5n−10=3n2−17n−10
So the equation becomes:3n2−17n−10(n+2)(n−4)=2n2−14n(n+2)(n−4)\frac{3n^2 – 17n – 10}{(n + 2)(n – 4)} = \frac{2n^2 – 14n}{(n + 2)(n – 4)}(n+2)(n−4)3n2−17n−10=(n+2)(n−4)2n2−14n
Since the denominators are the same, we equate the numerators:3n2−17n−10=2n2−14n3n^2 – 17n – 10 = 2n^2 – 14n3n2−17n−10=2n2−14n
Step 4: Bring all terms to one side
3n2−17n−10−2n2+14n=03n^2 – 17n – 10 – 2n^2 + 14n = 03n2−17n−10−2n2+14n=0n2−3n−10=0n^2 – 3n – 10 = 0n2−3n−10=0
Step 5: Solve the quadratic equation
Use the quadratic formula:n=−(−3)±(−3)2−4(1)(−10)2(1)=3±9+402=3±492n = \frac{-(-3) \pm \sqrt{(-3)^2 – 4(1)(-10)}}{2(1)} = \frac{3 \pm \sqrt{9 + 40}}{2} = \frac{3 \pm \sqrt{49}}{2}n=2(1)−(−3)±(−3)2−4(1)(−10)=23±9+40=23±49n=3±72⇒n=102=5orn=−42=−2n = \frac{3 \pm 7}{2} \Rightarrow n = \frac{10}{2} = 5 \quad \text{or} \quad n = \frac{-4}{2} = -2n=23±7⇒n=210=5orn=2−4=−2
Step 6: Check for extraneous solutions
The original equation contains denominators n+2n + 2n+2 and n−4n – 4n−4. We must exclude values that make any denominator zero.
- n=−2n = -2n=−2 makes n+2=0n + 2 = 0n+2=0 → Not allowed
- n=4n = 4n=4 makes n−4=0n – 4 = 0n−4=0 → Not allowed
Since n=−2n = -2n=−2 is not valid, we reject it.
✅ Final Answer:
n=5\boxed{n = 5}n=5
Explanation
To solve the equation 3nn+2−5n−4=2n2−14nn2−2n−8\frac{3n}{n+2} – \frac{5}{n-4} = \frac{2n^2 – 14n}{n^2 – 2n – 8}n+23n−n−45=n2−2n−82n2−14n, we start by factoring the denominator on the right. The quadratic n2−2n−8n^2 – 2n – 8n2−2n−8 factors as (n−4)(n+2)(n – 4)(n + 2)(n−4)(n+2). Recognizing this is helpful because it matches the denominators on the left. We then rewrite each term so that they all have a common denominator: (n+2)(n−4)(n + 2)(n – 4)(n+2)(n−4). This allows us to combine and compare the numerators directly.
We expand the numerators: 3n(n−4)3n(n – 4)3n(n−4) gives 3n2−12n3n^2 – 12n3n2−12n, and 5(n+2)5(n + 2)5(n+2) gives 5n+105n + 105n+10. Subtracting the second expression from the first gives 3n2−17n−103n^2 – 17n – 103n2−17n−10. The right-hand side numerator remains 2n2−14n2n^2 – 14n2n2−14n. Now that both sides of the equation have the same denominator, we equate the numerators: 3n2−17n−10=2n2−14n3n^2 – 17n – 10 = 2n^2 – 14n3n2−17n−10=2n2−14n.
Bringing all terms to one side yields the quadratic n2−3n−10=0n^2 – 3n – 10 = 0n2−3n−10=0. Solving with the quadratic formula, we find n=5n = 5n=5 and n=−2n = -2n=−2. However, we must check for values that make any denominator in the original equation zero. Here, n=−2n = -2n=−2 makes the term n+2=0n + 2 = 0n+2=0, which is undefined. So we reject that solution.
The only valid solution is n=5n = 5n=5, which satisfies all parts of the original equation without making any denominator zero.
