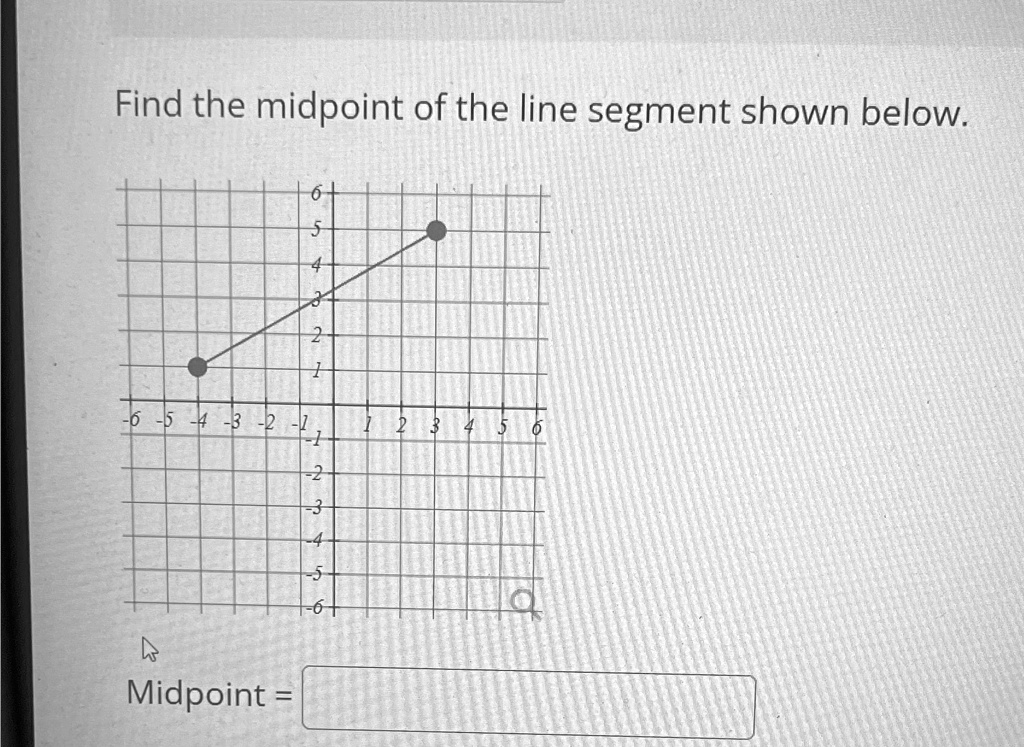
Find the midpoint of the line segment shown below. Midpoint =
The Correct Answer and Explanation is:
The midpoint of the line segment with endpoints at (-4, 0) and (4, 4) is (0, 2).
To understand why, we use the midpoint formula from coordinate geometry. The formula gives the coordinates of the point exactly halfway between two other points. Mathematically, if the endpoints of a segment are (x1,y1)(x_1, y_1) and (x2,y2)(x_2, y_2), the midpoint (Mx,My)(M_x, M_y) is calculated using:
Mx=x1+x22,My=y1+y22M_x = \frac{x_1 + x_2}{2}, \quad M_y = \frac{y_1 + y_2}{2}
Plugging in the given values:
Mx=−4+42=02=0,My=0+42=42=2M_x = \frac{-4 + 4}{2} = \frac{0}{2} = 0, \quad M_y = \frac{0 + 4}{2} = \frac{4}{2} = 2
So the coordinates of the midpoint are (0,2)(0, 2).
Visually, this means that the point lies directly between the two endpoints along both the horizontal and vertical directions. Horizontally, the points extend from -4 to 4, and halfway between them is 0. Vertically, from 0 to 4, the value halfway is 2. This spatial balance is what makes the midpoint central to the segment.
In coordinate geometry, midpoints have a range of applications. They are useful in bisecting line segments, finding centers of diagonals in quadrilaterals, or even dividing spaces symmetrically. Understanding how to compute the midpoint strengthens one’s grasp of spatial relationships and symmetry, both of which are critical for more advanced geometry topics.
This foundational concept also supports practical applications in design, mapping, and engineering, where balance and symmetry are often required. In essence, the midpoint represents a simple but powerful geometric tool.
