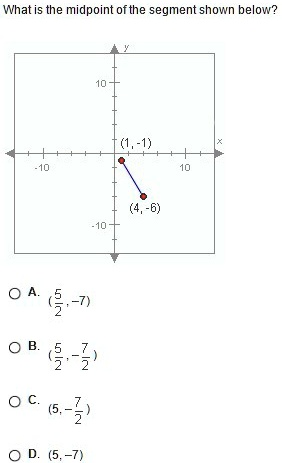
The Correct Answer and Explanation is:
The correct answer is B. (5/2, -7/2).
To find the midpoint of a line segment given its endpoints, we use the midpoint formula:
Midpoint=(x1+x22,y1+y22)\text{Midpoint} = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)
In this case, the endpoints provided are (1, -1) and (4, -6). Assigning values:
- x1=1x_1 = 1, y1=−1y_1 = -1
- x2=4x_2 = 4, y2=−6y_2 = -6
Substitute into the formula:
Midpoint=(1+42,−1+(−6)2)=(52,−72)\text{Midpoint} = \left( \frac{1 + 4}{2}, \frac{-1 + (-6)}{2} \right) = \left( \frac{5}{2}, \frac{-7}{2} \right)
This results in a midpoint of (5/2, -7/2).
The importance of this computation lies in its simplicity and broad applicability. The midpoint gives the exact center between two locations in a coordinate system. It represents an average in both dimensions. In real-world terms, if two objects lie at those coordinates, the midpoint would be the location equidistant from both. Engineers and architects often use midpoint calculations when designing structures to ensure balance. In navigation, determining midpoints can help in plotting central waypoints.
Furthermore, grasping midpoint calculations enhances one’s understanding of linear relationships and distance. It plays a foundational role in analytic geometry and supports more complex concepts like vector analysis, centroids in physics, and bisectors in geometry. By practicing this type of problem, learners strengthen their grasp of spatial reasoning and reinforce number manipulation skills. It also promotes precision, since small errors in arithmetic can lead to incorrect results. Understanding the midpoint formula offers more than just a correct answer—it provides a methodical approach to locating balance between any two points on the Cartesian plane.
