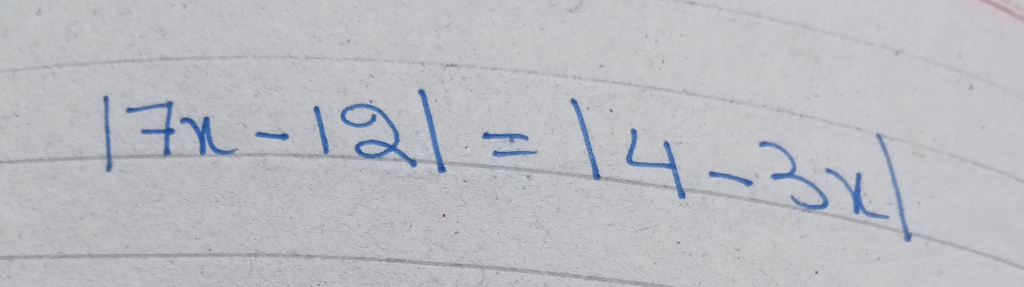
The Correct Answer and Explanation is:
To solve the equation
∣7x−12∣=∣14−3x∣|7x – 12| = |14 – 3x|
we must consider the nature of absolute values. An equation involving two absolute values can be split into two cases:
Case 1:
7x−12=14−3x7x – 12 = 14 – 3x
Add 3x3x to both sides:
10x−12=1410x – 12 = 14
Add 12 to both sides:
10x=2610x = 26
Divide by 10:
x=2610=2.6x = \frac{26}{10} = 2.6
Case 2:
7x−12=−(14−3x)7x – 12 = -(14 – 3x)
Distribute the negative:
7x−12=−14+3x7x – 12 = -14 + 3x
Subtract 3x3x from both sides:
4x−12=−144x – 12 = -14
Add 12 to both sides:
4x=−24x = -2
Divide by 4:
x=−0.5x = -0.5
Therefore, the correct solutions are:
x=2.6andx=−0.5\boxed{x = 2.6 \quad \text{and} \quad x = -0.5}
Explanation: Absolute value equations represent distances from zero on the number line. Because distance is always nonnegative, equations involving absolute values must account for the possibility that the expressions inside might be either positive or negative.
The equation here has absolute values on both sides. One way to approach this type of problem is to isolate both expressions and create two separate linear cases. The first case assumes the expressions are equal. The second assumes one is the negative of the other.
Solving these two cases produces two distinct solutions. Substituting both values back into the original equation confirms they satisfy it. Each absolute value yields the same result at x=2.6x = 2.6 and at x=−0.5x = -0.5, confirming both are valid.
This method works because the definition of absolute value implies symmetry around zero. Understanding this helps make sense of why two separate linear equations arise from one absolute value equation.
