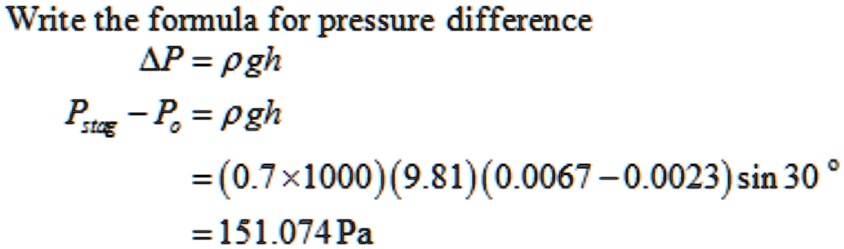
The Correct Answer and Explanation is:
The correct answer is: 151.074 Pa
To determine the pressure difference between the stagnation pressure and the static pressure, we apply the hydrostatic pressure formula:
ΔP=ρgh\Delta P = \rho g h
In this case, the change in height is not a vertical column but an inclined difference. Therefore, the vertical component of the height must be calculated using trigonometry. The full expression becomes:
Pstag−P0=ρg(h2−h1)sin(θ)P_{\text{stag}} – P_0 = \rho g (h_2 – h_1) \sin(\theta)
Substituting the given values:
- Density ρ=0.7×1000=700 kg/m3\rho = 0.7 \times 1000 = 700 \, \text{kg/m}^3
- Acceleration due to gravity g=9.81 m/s2g = 9.81 \, \text{m/s}^2
- Difference in height h=0.0067−0.0023=0.0044 mh = 0.0067 – 0.0023 = 0.0044 \, \text{m}
- Incline angle θ=30∘\theta = 30^\circ
We plug in the values:
Pstag−P0=700×9.81×0.0044×sin(30∘)P_{\text{stag}} – P_0 = 700 \times 9.81 \times 0.0044 \times \sin(30^\circ)
=700×9.81×0.0044×0.5= 700 \times 9.81 \times 0.0044 \times 0.5
=151.074 Pa= 151.074 \, \text{Pa}
This pressure difference arises due to the hydrostatic principle, which states that pressure increases with depth in a fluid due to the weight of the fluid above. In this scenario, the pressure difference is oriented along an inclined manometer, so the vertical component of the height difference is used. Multiplying this height by the density and gravitational acceleration gives the pressure exerted due to the fluid column. The sine function adjusts the effective height since the fluid columns are not perfectly vertical. This principle is commonly used in fluid mechanics and aerodynamics to measure velocity-related pressures and is a foundation of Pitot-static tube analysis.
