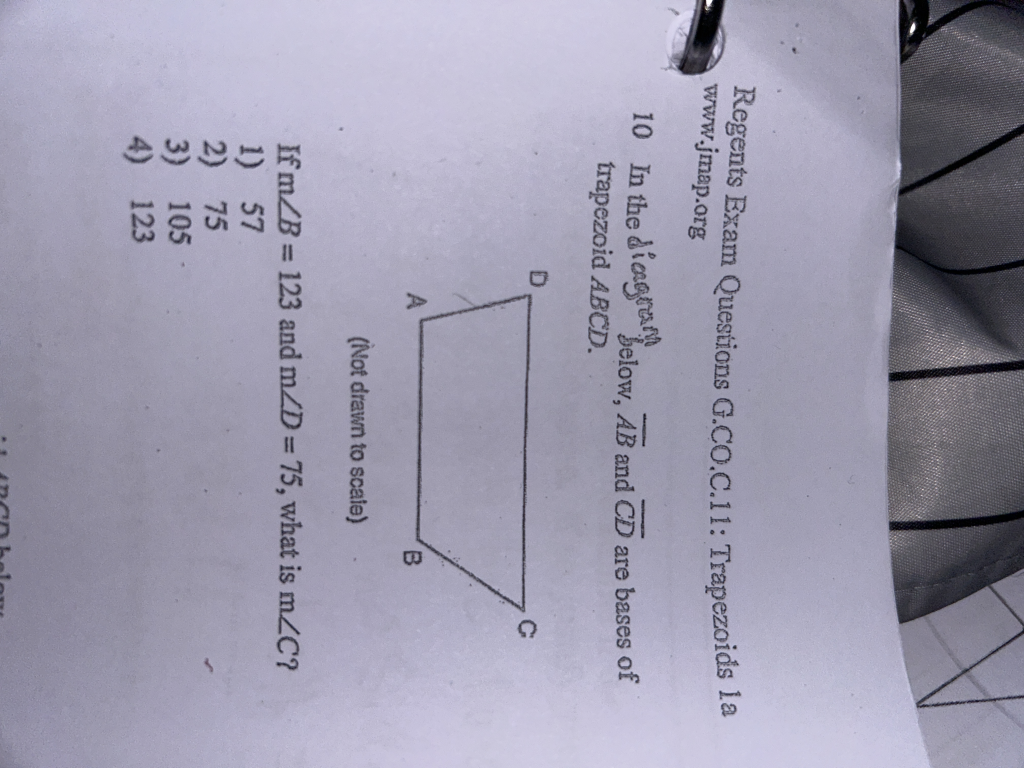
Regents Exam Questions G.CO.C.11: Trapezoids 1a www.jmap.org 10
The Correct Answer and Explanation is:
We are given a trapezoid ABCDABCDABCD, where AB‾\overline{AB}AB and CD‾\overline{CD}CD are the bases. The angles provided are:
- ∠B=123∘\angle B = 123^\circ∠B=123∘
- ∠D=75∘\angle D = 75^\circ∠D=75∘
We are asked to find m∠Cm\angle Cm∠C.
In any quadrilateral, the sum of the interior angles is always 360 degrees. So:m∠A+m∠B+m∠C+m∠D=360∘m\angle A + m\angle B + m\angle C + m\angle D = 360^\circm∠A+m∠B+m∠C+m∠D=360∘
We are given:m∠B=123∘,m∠D=75∘m\angle B = 123^\circ,\quad m\angle D = 75^\circm∠B=123∘,m∠D=75∘
Let’s substitute into the equation:m∠A+123+m∠C+75=360m\angle A + 123 + m\angle C + 75 = 360m∠A+123+m∠C+75=360
Simplify:m∠A+m∠C=360−(123+75)=162∘m\angle A + m\angle C = 360 – (123 + 75) = 162^\circm∠A+m∠C=360−(123+75)=162∘
Since ABABAB and CDCDCD are the bases, angles AAA and DDD are same-side interior angles, and BBB and CCC are same-side interior angles. In trapezoids, same-side interior angles between the bases are supplementary. That means:m∠B+m∠C=180∘m\angle B + m\angle C = 180^\circm∠B+m∠C=180∘
We already know:m∠B=123∘m\angle B = 123^\circm∠B=123∘
So:123+m∠C=180⇒m∠C=57∘123 + m\angle C = 180 \Rightarrow m\angle C = 57^\circ123+m∠C=180⇒m∠C=57∘
Final Answer: 1) 57
Explanation
In a trapezoid, two of the sides are parallel. These parallel sides form what are known as base angles. A special property of trapezoids is that any pair of consecutive angles between a leg and the parallel bases are supplementary. This means their measures add up to 180 degrees. In trapezoid ABCDABCDABCD, sides AB‾\overline{AB}AB and CD‾\overline{CD}CD are given as the bases. Therefore, angles BBB and CCC lie between the same leg and these parallel sides, which makes them consecutive interior angles. That means they are supplementary.
We are given that angle BBB measures 123 degrees. To find angle CCC, we use the supplementary angle rule:m∠B+m∠C=180∘⇒123+m∠C=180⇒m∠C=180−123=57∘m\angle B + m\angle C = 180^\circ \Rightarrow 123 + m\angle C = 180 \Rightarrow m\angle C = 180 – 123 = 57^\circm∠B+m∠C=180∘⇒123+m∠C=180⇒m∠C=180−123=57∘
We can also verify this by adding up all the interior angles of the quadrilateral. All four interior angles of any quadrilateral add up to 360 degrees. Knowing angle B=123∘B = 123^\circB=123∘ and angle D=75∘D = 75^\circD=75∘, we can find the sum of the remaining two angles AAA and CCC as:m∠A+m∠C=360−(123+75)=162∘m\angle A + m\angle C = 360 – (123 + 75) = 162^\circm∠A+m∠C=360−(123+75)=162∘
This confirms our result again, since angle A=105∘A = 105^\circA=105∘ and angle C=57∘C = 57^\circC=57∘ would satisfy this. Therefore, the correct measure of angle CCC is 57 degrees.
