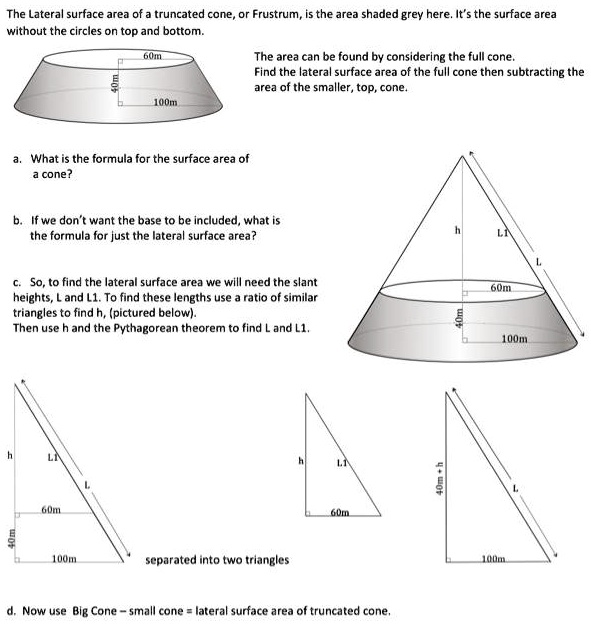
The Lateral surface area of a truncated cone, or Frustrum, is the area shaded grey here. It’s the surface area without the circles on top and bottom. The area can be found by considering the full cone. Find the lateral surface area of the full cone then subtracting the area of the smaller, top, cone. a. What is the formula for the surface area of a cone? b. If we don’t want the base to be included, what is the formula for just the lateral surface area? c. So, to find the lateral surface area we will need the slant heights, L and L1. To find these lengths use a ratio of similar triangles to find h, (pictured below). Then use h and the Pythagorean theorem to find L and L1. d. Now use Big Cone – small cone = lateral surface area of truncated cone.
The Correct Answer and Explanation is:
a. Formula for the surface area of a cone:
The total surface area of a cone is
A=πr(r+L)A = \pi r (r + L)
where rr is the radius and LL is the slant height.
b. Lateral surface area (excluding the base):
Alateral=πrLA_{\text{lateral}} = \pi r L
c. Finding slant heights using similar triangles and Pythagorean theorem:
From the diagram:
- Big cone radius = 100 m
- Small cone radius = 60 m
- Truncated height = 40 m
Use similar triangles to find full height hh of the big cone:
h40=10060⇒h=100⋅4060=66.67 m\frac{h}{40} = \frac{100}{60} \Rightarrow h = \frac{100 \cdot 40}{60} = 66.67 \text{ m}
Now the height of the small cone is h−40=26.67 mh – 40 = 26.67 \text{ m}
Use Pythagorean theorem for slant heights:
For big cone:
L=1002+66.672=10000+4444.89=14444.89≈120.19 mL = \sqrt{100^2 + 66.67^2} = \sqrt{10000 + 4444.89} = \sqrt{14444.89} \approx 120.19 \text{ m}
For small cone:
L1=602+26.672=3600+711.11=4311.11≈65.66 mL_1 = \sqrt{60^2 + 26.67^2} = \sqrt{3600 + 711.11} = \sqrt{4311.11} \approx 65.66 \text{ m}
d. Lateral surface area of frustum:
Afrustum=πrL−πr1L1=π(100)(120.19)−π(60)(65.66)A_{\text{frustum}} = \pi r L – \pi r_1 L_1 = \pi (100)(120.19) – \pi (60)(65.66)
Afrustum=12019π−3939.6π=8079.4πA_{\text{frustum}} = 12019\pi – 3939.6\pi = 8079.4\pi
Afrustum≈25376.3 m2A_{\text{frustum}} \approx 25376.3 \text{ m}^2
Explanation
To calculate the lateral surface area of a truncated cone, also called a frustum, we begin by recognizing that the curved surface is the difference between the lateral areas of two full cones: a larger one and a smaller one at the top. The curved surface does not include the circular bases. First, the formula for the total surface area of a cone is πr(r+L)\pi r (r + L), but since we are only interested in the curved area, we use πrL\pi r L where LL is the slant height.
To compute the slant heights, we use properties of similar triangles. Since the cones are similar and the frustum has a vertical height of 40 meters, we apply a ratio of the radii to find the full height of the large cone: h40=10060\frac{h}{40} = \frac{100}{60}. This gives h=66.67h = 66.67 meters. The height of the smaller, top cone is then 66.67−40=26.6766.67 – 40 = 26.67 meters.
Next, we use the Pythagorean theorem. The slant height of the large cone is calculated from the radius and height as the hypotenuse. Similarly, we find the slant height for the smaller cone. Finally, we apply the lateral area formula for both cones and subtract the smaller from the larger: πrL−πr1L1\pi r L – \pi r_1 L_1. This results in the lateral area of the frustum being approximately 25376.3 square meters.
